题目内容
【题目】若椭圆![]() :
:![]() 上有一动点
上有一动点![]() ,
,![]() 到椭圆
到椭圆![]() 的两焦点
的两焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,
,![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,
,![]() (
(![]() 为坐标原点)且
为坐标原点)且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .
.
(2) (-2,![]() )∪(
)∪(![]() ,2).
,2).
【解析】分析:(I)由椭圆的定义及到直线![]() 的最大距离为
的最大距离为![]() 列方程可求得
列方程可求得![]() 和
和![]() 的值,从而可求得椭圆的方程;(II)设椭圆的方程,代入椭圆的方程,由
的值,从而可求得椭圆的方程;(II)设椭圆的方程,代入椭圆的方程,由![]() 取得
取得![]() 的取值范围,利用韦达定理及向量的坐标运算求得
的取值范围,利用韦达定理及向量的坐标运算求得![]() 点坐标,代入椭圆方程,求得
点坐标,代入椭圆方程,求得![]() ,由
,由![]() ,即可求得
,即可求得![]() 的取值范围.
的取值范围.
详解:(I)由已知得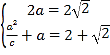 ,∴
,∴![]() ,
,![]()
![]() ,
,
所以椭圆的方程为:![]() .
.
(II)l的斜率必须存在,即设l:![]() ,
,
联立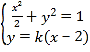 ,消去y整理得
,消去y整理得![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,
,![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() ,
,
而![]() +
+![]() =
=![]() ,设P(x,y),
,设P(x,y),
∴![]() ∴
∴ ,
,
而P在椭圆C上,∴![]() ,
,
∴![]() (*),又∵
(*),又∵![]() ,
,
![]() ,
,
解之,得![]() ,∴
,∴![]() ,
,
再将(*)式化为![]()
![]() ,将
,将![]() 代入
代入
得![]() ,即
,即![]() 或
或![]() ,
,
则t的取值范围是(-2,![]() )∪(
)∪(![]() ,2)
,2)

练习册系列答案
相关题目