题目内容
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2, ![]() ,E为CD的中点,点F在线段PB上.
,E为CD的中点,点F在线段PB上. 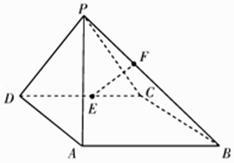
(Ⅰ)求证:AD⊥PC;
(Ⅱ)试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
【答案】解:(Ⅰ)证明:在平行四边形ABCD中,连接AC, 因为 ![]() ,BC=2,∠ABC=45°,
,BC=2,∠ABC=45°,
由余弦定理得 ![]() ,∴AC=2,
,∴AC=2,
∴AC2+BC2=AB2 , ∴BC⊥AC,
又AD∥BC,∴AD⊥AC,
∵AD=AP=2, ![]() ,∴AD2+AP2=DP2 , ∴PA⊥AD,
,∴AD2+AP2=DP2 , ∴PA⊥AD,
又AP∩AC=A,AP平面PAC,AC平面PAC,
∴AD⊥平面PAC,∵PC平面PAC,
∴AD⊥PC.
(Ⅱ)∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,PA⊥AD,PA平面PAD,
∴PA⊥底面ABCD,
以A为原点,以直线DA,AC,AP坐标轴建立如图所示空间直角坐标系A﹣xyz,
则A(0,0,0),D(﹣2,0,0),C(0,2,0),B(2,2,0),E(﹣1,1,0),P(0,0,2),
所以 ![]() ,
, ![]() ,
, ![]() ,设
,设 ![]() (λ∈[0,1]),
(λ∈[0,1]),
则 ![]() ,F(2λ,2λ,﹣2λ+2),
,F(2λ,2λ,﹣2λ+2),
∴ ![]() ,
,
平面ABCD的一个法向量为 ![]() =(0,0,1).
=(0,0,1).
设平面PDC的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,
,
∴ ![]() ,令x=1,得
,令x=1,得 ![]() =(1,﹣1,﹣1).
=(1,﹣1,﹣1).
∵直线EF与平面PDC所成的角和此直线与平面ABCD所成的角相等,
∴|cos< ![]() >|=|cos<
>|=|cos< ![]() >|,
>|,
即 ![]() =
=  ,∴2﹣2λ=
,∴2﹣2λ= ![]() ,解得
,解得 ![]() ,
,
∴当 ![]() 时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
【解析】(I)利用勾股定理的逆定理证明AD⊥AP,BC⊥AC,从而AD⊥平面PAC,得出AD⊥PC;(II)由面面垂直的性质可得AP⊥平面ABCD,建立空间坐标系,设 /span>![]() =λ,求出平面PCD的法向量
=λ,求出平面PCD的法向量 ![]() 和平面ABCD的法向量
和平面ABCD的法向量 ![]() ,令|cos<
,令|cos< ![]() >|=|cos<
>|=|cos< ![]() >|,解出λ即可.
>|,解出λ即可.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系和空间角的异面直线所成的角的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.

【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002,…,800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;(下面摘取了第7行到第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100人的数学与地理的水平测试成绩如下表:
人 数 | 数 学 | |||
优 秀 | 良 好 | 及 格 | ||
地 理 | 优 秀 | 7 | 20 | 5 |
良 好 | 9 | 18 | 6 | |
及 格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() .
.
①若在该样本中,数学成绩优秀率是![]() ,求
,求![]() 的值:
的值:
②在地理成绩及格的学生中,已知![]() ,
,![]() ,求数学成绩优秀的人数比及格的人数少的概率.
,求数学成绩优秀的人数比及格的人数少的概率.
【题目】某汽车公司对最近6个月内的市场占有率进行了统计,结果如表;
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() 两款车扩大市场,
两款车扩大市场, ![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:
车型 | 报废年限(年) | 合计 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/辆 |
| 15 | 40 | 35 | 10 | 100 | 800元/辆 |
平均每辆车每年可为公司带来收入![]() 元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数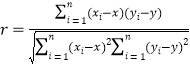 ;
;
回归直线方程为![]() ,其中
,其中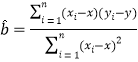 ,
,![]() .
.