题目内容
【题目】已知函数F(x)=lnx(x>1)的图象与函数G(x)的图象关于直线y=x对称,若函数f(x)=(k﹣1)x﹣G(﹣x)无零点,则实数k的取值范围是( )
A.(1﹣e,1)
B.(1﹣e,∞)
C.(1﹣e,1]
D.(﹣∞,1﹣e)∪[1,+∞)
【答案】B
【解析】解:函数F(x)=lnx(x>1)的图象与函数G(x)的图象关于直线y=x对称, 可得G(x)=ex , (x>1),
则G(﹣x)=e﹣x , (x<﹣1),
函数f(x)=(k﹣1)x﹣G(﹣x)无零点,
即f(x)=(k﹣1)x﹣e﹣x , 没有零点,也就是y=(k﹣1)x,与y=e﹣x , (x<﹣1),
没有公共点.
y′=﹣e﹣x , 设切点坐标为:(m,e﹣m),
可得:k﹣1=﹣e﹣m= ![]() ,解得m=﹣1,
,解得m=﹣1,
此时k=1﹣e,
函数f(x)=(k﹣1)x﹣G(﹣x)无零点,则k>1﹣e.
故选:B.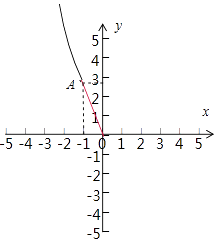

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目