��Ŀ����
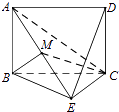
����Ŀ��ij������һ�����Ž������䴰�������ͼ��ʾ��Բ![]() ��Բ�������
��Բ�������![]() �Խ��ߵĽ����غϣ���Բ�����������������(
�Խ��ߵĽ����غϣ���Բ�����������������(![]() Ϊ���е�)�������������ཻ(
Ϊ���е�)�������������ཻ(![]() ��
�� ![]() Ϊ������������)��ͼ����Ӱ����Ϊ�����������ಿ��Ϊ����������֪Բ�İ뾶Ϊ1m����
Ϊ������������)��ͼ����Ӱ����Ϊ�����������ಿ��Ϊ����������֪Բ�İ뾶Ϊ1m����![]() ����
����![]() ������������Ϊ
������������Ϊ![]() ��
��
��1����![]() ����
����![]() �ĺ�����ϵʽ���������������
�ĺ�����ϵʽ���������������
��2���������Ҫ������������δ���������ֵԽ��Խ�������ñ�ֵ���ʱ�����![]() �ij�����
�ij�����
���𰸡���1����2��
���������������: ���������ʾ��������߶γ��ȣ��ٷֱ��������κ�����������Ӷ���ʾ����������ٸ�������Ҫ����������Ķ������������ʾ������ȡ�����![]() ���������о�����������������ֵ.
���������о�����������������ֵ.
�������:��1������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��
����![]() ��
��
![]() ��
��
����![]() ��
��
��Ϊ![]() ������
������![]() �����Զ�����Ϊ
�����Զ�����Ϊ![]() ��
��
��2�����δ�������Ϊ![]() ��
��
������������δ���������ֵΪ![]() ����10��
����10��
��![]() ��
�� ![]() ��
��
��![]()
 ��
��
��Ϊ![]() ������
������![]() ������
������![]() ����
����![]() ��
��
���Ժ���![]() ��
��![]() �ϵ�������
�ϵ�������
���Ե�![]() ʱ��
ʱ�� ![]() �����ֵ
�����ֵ![]() ����ʱ
����ʱ![]() (m)��
(m)��
�𣺣�1��![]() ����
����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��������Ϊ
��������Ϊ![]() ��
��
��2������������δ���������ֵ���ʱ�� ![]() �ij���Ϊ1m��
�ij���Ϊ1m��

����Ŀ��������Ʊ��˫ɫ���к���ĺ�����Դ�01��02��03������32��33��33����λ������ѡȡ��С��������ͼ��ʾ���������ѡȡ��ɫ���6�����룬ѡȡ�����Ǵӵ�1�е�9�к͵�10�е����ֿ�ʼ����������ѡȡ�������֣�����ĸ���ѡ�еĺ�ɫ�����Ϊ�� ��
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16