题目内容
20.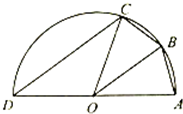 如图所示,AD是半径为5的半圆O的直径,B,C是半圆O上的两点,cos∠AOB=$\frac{4}{5}$,AB=BC,
如图所示,AD是半径为5的半圆O的直径,B,C是半圆O上的两点,cos∠AOB=$\frac{4}{5}$,AB=BC,(Ⅰ)求cos∠ABC的值
(Ⅱ)求$\overrightarrow{BA}•\overrightarrow{BC}$的值.
分析 (I)由AB=BC,可得∠AOB=∠COB=∠ADC.利用A,B,C,D四点共圆,可得∠ABC=180°-∠ADC,即可得出.
(II)在△AOB中,由余弦定理可得:AB2=OA2+OB2-2OA•OBcos∠AOB.即可得出$\overrightarrow{BA}•\overrightarrow{BC}$=$|\overrightarrow{BA}||\overrightarrow{BC}|$cos∠ABC.
解答 解:(I)∵AB=BC,∴∠AOB=∠COB=∠ADC.
又∵A,B,C,D四点共圆,∴∠ABC=180°-∠ADC,
∴cos∠ABC=cos(180°-∠ADC)=-cos∠ADC=-cos∠AOB=-$\frac{4}{5}$.
(II)在△AOB中,由余弦定理可得:AB2=OA2+OB2-2OA•OBcos∠AOB=$25+25-2×5×5×\frac{4}{5}$=10,
∴|AB|=|BC|=$\sqrt{10}$.
∴$\overrightarrow{BA}•\overrightarrow{BC}$=$|\overrightarrow{BA}||\overrightarrow{BC}|$cos∠ABC=$\sqrt{10}×\sqrt{10}×(-\frac{4}{5})$=-8.
点评 本题考查了向量的数量积运算性质、圆的性质、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.已知等差数列{an}的公差为d,前n项和为Sn,若S6>S7>S5,则下列命题错误的是( )
| A. | d<0 | B. | S11>0 | ||
| C. | {Sn}中的最大项为S11 | D. | |a6|>|a7| |
8.已知向量$\overrightarrow{a}$=(0,2$\sqrt{3}$),b=(1,$\sqrt{3}$),则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -3 |
15.在△ABC中,已知∠A=45°,∠B=60°,a=2,则b=( )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | 3$\sqrt{6}$ | D. | 4$\sqrt{6}$ |
12.若定义域为R的奇函数f(x)满足f(x+2)=f(x),且在(-3,-2)上单调递减,则( )
| A. | f($\frac{3}{4}$)<f($\frac{1}{2}$) | B. | f($\frac{3}{4}$)>f($\frac{1}{2}$) | ||
| C. | f($\frac{3}{4}$)=f($\frac{1}{2}$) | D. | f($\frac{3}{4}$)与f($\frac{1}{2}$)的大小不确定 |
10.已知A(3,-1),B(5,-2),点P在直线x+y=0上,若使|PA|+|PB|取最小值,则点P的坐标是( )
| A. | (1,-1) | B. | (-1,1) | C. | ($\frac{13}{5}$,-$\frac{13}{5}$) | D. | (-2,2) |