题目内容
19.已知函数f(x)=|x2-1|,g(x)=x2+ax+2,x∈R,若函数h(x)=f(x)+g(x)+2在(0,2)上有两个不同的零点x1,x2,则a的取值范围是$(-\frac{11}{2},-2\sqrt{6})$.分析 由h(x)=f(x)+g(x)+2,可得a的关系式,求出函数的值域,即可求实数a的取值范围.
解答 解:由h(x)=f(x)+g(x)+2,可得a=$\frac{-|{x}^{2}-1|-{x}^{2}-4}{x}$=$\left\{\begin{array}{l}{-\frac{5}{x},x∈(0,1)}\\{-(2x+\frac{3}{x}),x∈[1,2]}\end{array}\right.$
x∈(0,1),a=-$\frac{5}{x}$单调递增,且值域为(-∞,-5);
x∈[1,2),k(x)=-(2x+$\frac{3}{x}$)先增后减,
∵k(1)=-5,k(x)max=-2$\sqrt{6}$,k(2)=-$\frac{11}{2}$,
∴-$\frac{11}{2}$<a<-2$\sqrt{6}$.
综上,a的取值范围是$(-\frac{11}{2},-2\sqrt{6})$.
故答案为:$(-\frac{11}{2},-2\sqrt{6})$.
点评 本题考查解不等式,考查分离参数法的运用,考查函数的值域,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
11.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是( )
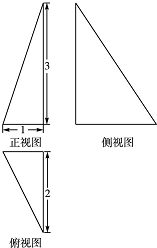

| A. | 1 m3 | B. | 2 cm3 | C. | 3 cm3 | D. | 6 cm3 |