题目内容
【题目】在正方体![]() 中,点
中,点![]() 平面
平面![]() ,点
,点![]() 是线段
是线段![]() 的中点,若
的中点,若![]() ,则当
,则当![]() 的面积取得最小值时,
的面积取得最小值时,![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据![]() 分析出点
分析出点![]() 在直线
在直线![]() 上,当
上,当![]() 的面积取得最小值时,线段
的面积取得最小值时,线段![]() 的长度为点
的长度为点![]() 到直线
到直线![]() 的距离,即可求得面积关系.
的距离,即可求得面积关系.
先证明一个结论P:若平面外的一条直线l在该平面内的射影垂直于面内的直线m,则l⊥m,
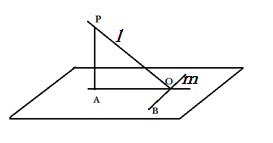
即:已知直线l在平面内的射影为直线OA,OA⊥OB,求证:l⊥OB.
证明:直线l在平面内的射影为直线OA,
不妨在直线l上取点P,使得PA⊥OB,OA⊥OB,OA,PA是平面PAO内两条相交直线,
所以OB⊥平面PAO,![]() 平面PAO,
平面PAO,
所以PO⊥OB,即l⊥OB.以上这就叫做三垂线定理.
如图所示,取![]() 的中点
的中点![]() ,
,
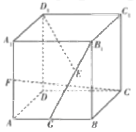
正方体中:![]() ,
,![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,
由三垂线定理可得:![]() ,
,
![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,![]()
由三垂线定理可得:![]() ,
,![]() 与
与![]() 是平面
是平面![]() 内两条相交直线,
内两条相交直线,
所以![]() 平面
平面![]() ,
,
∴当点![]() 在直线
在直线![]() 上时,
上时,![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 的面积取最小值时,
的面积取最小值时,
线段![]() 的长度为点
的长度为点![]() 到直线
到直线![]() 的距离,
的距离,
∴线段![]() 长度的最小值为
长度的最小值为![]() ,
,
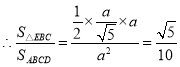 .
.
故选:D.

练习册系列答案
相关题目