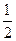题目内容
已知函数f(x)在(-∞,0)∪(0,+∞)上有定义,且在(0,+∞)上是增函数,f(1)=0,又g(θ)=sin2θ-mcosθ-2m,θ∈[0,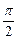 ],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
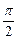 ],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.M∩N={m|m>4-2 }
}
 }
}∵f(x)是奇函数,且在(0,+∞)上是增函数,
∴f(x)在(-∞,0)上也是增函数.
又f(1)=0,∴f(-1)=-f(1)=0,从而,当f(x)<0时,有x<-1或0<x<1,
则集合N={m|f[g(θ)]<θ= ={m|g(θ)<-1或0<g(θ)<1
={m|g(θ)<-1或0<g(θ)<1 ,
,
∴M∩N={m|g(θ)<-1 .
.
由g(θ)<-1,得cos2θ>m(cosθ-2)+2,θ∈[0,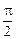 ],
],
令x=cosθ,x∈[0,1]得 x2>m(x-2)+2,x∈[0,1],
x2>m(x-2)+2,x∈[0,1],
令①: y1=x2,x∈[0,1]及②y2=m(m-2)+2,
显然①为抛物线一段,②是过(2,2)点的直线系,
在同一坐标系内由x∈[0,1]得y1>y2.
∴m>4-2 ,故M∩N={m|m>4-2
,故M∩N={m|m>4-2 }.
}.
∴f(x)在(-∞,0)上也是增函数.
又f(1)=0,∴f(-1)=-f(1)=0,从而,当f(x)<0时,有x<-1或0<x<1,
则集合N={m|f[g(θ)]<θ=
 ={m|g(θ)<-1或0<g(θ)<1
={m|g(θ)<-1或0<g(θ)<1 ,
,∴M∩N={m|g(θ)<-1
 .
. 由g(θ)<-1,得cos2θ>m(cosθ-2)+2,θ∈[0,
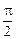 ],
],令x=cosθ,x∈[0,1]得
 x2>m(x-2)+2,x∈[0,1],
x2>m(x-2)+2,x∈[0,1],令①: y1=x2,x∈[0,1]及②y2=m(m-2)+2,
显然①为抛物线一段,②是过(2,2)点的直线系,
在同一坐标系内由x∈[0,1]得y1>y2.
∴m>4-2
 ,故M∩N={m|m>4-2
,故M∩N={m|m>4-2 }.
}. 
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 是在
是在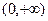 上每一点均可导的函数,若
上每一点均可导的函数,若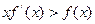 在
在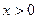 时恒成立.
时恒成立.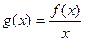 在
在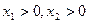 时,有
时,有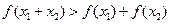 ;
;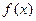 对一切实数
对一切实数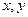 均有
均有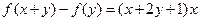 成立,
成立,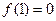 .
.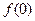 的值;
的值;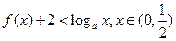 恒成立时,求
恒成立时,求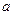 的取值范围
的取值范围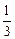 ),f(
),f(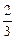 ),f(1)的大小关系_________.
),f(1)的大小关系_________. 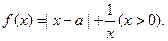 (I)当a=1时,求
(I)当a=1时,求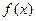 的最小值;(II)若
的最小值;(II)若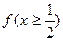 恒成立,求a的取值范围。
恒成立,求a的取值范围。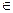 R都有f(a+b)=
R都有f(a+b)=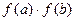 ,且f(1)=2,则
,且f(1)=2,则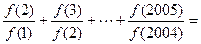 __________
__________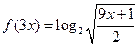 ,则
,则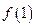 的值为
的值为