Question

【题目】已知A（-，0），B（0，-），其中k≠0且k≠±1，直线l经过点P(1，0)和AB的中点.

(1)求证：A，B关于直线l对称.

(2)当1<k<时，求直线l在y轴上的截距b的取值范围.

Answer 1

【答案】（1）证明见解析；（2）（-1，-）

【解析】试题分析：（1）由题意只需证明和垂直即可，有斜率公式可得和的斜率，得到，即可作出证明；

（2）可得直线在轴上的截距，由和函数的单调性，即可得到的取值范围.

试题解析：

(1)因为直线l经过AB的中点，

所以只需再证AB⊥l即可.

因为A-，0，B0，-，

所以AB的中点为-，-.

kAB=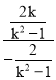=-k，kl==，

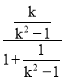所以kAB·kl=(-k)·=-1，

所以AB⊥l，

所以A，B关于直线l对称.

(2)kl=，所以直线l方程为y= (x-1)，其在y轴的截距b=-，

因为y=-在(0，+∞)上是单调增函数，

所以1<k<时，

-1<-<-即-1<b<-.

所以直线l在y轴上的截距b的取值范围是（-1，-）