题目内容
(满分13分)已知各项均为正数的数列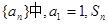 是数列
是数列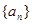 的前n项和,对任意
的前n项和,对任意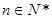 ,有2Sn=2
,有2Sn=2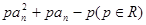 .
.
(Ⅰ)求常数p的值;
(Ⅱ)求数列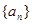 的通项公式;
的通项公式;
(Ⅲ)记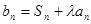 ,(
,(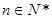 )若数列
)若数列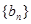 从第二项起每一项都比它的前一项大,求
从第二项起每一项都比它的前一项大,求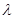 的取值范围.
的取值范围.
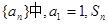 是数列
是数列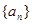 的前n项和,对任意
的前n项和,对任意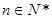 ,有2Sn=2
,有2Sn=2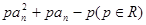 .
.(Ⅰ)求常数p的值;
(Ⅱ)求数列
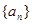 的通项公式;
的通项公式;(Ⅲ)记
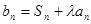 ,(
,(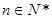 )若数列
)若数列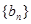 从第二项起每一项都比它的前一项大,求
从第二项起每一项都比它的前一项大,求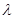 的取值范围.
的取值范围.(1) ;(2)
;(2) ;(3)
;(3) .
.
 ;(2)
;(2) ;(3)
;(3) .
.试题分析:(1)由
 及
及 ,得:
,得:

(2)由
 ①
①得
 (
( ,
, ) ②
) ②由②—①,得

即:


由于数列
 各项均为正数,
各项均为正数, 即
即  (
( ,
, )
) 数列
数列 是首项为
是首项为 ,公差为
,公差为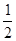 的等差数列,
的等差数列,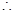 数列
数列 的通项公式是
的通项公式是 
(3)由题意,数列
 是递增的,
是递增的, ,即
,即
 对
对 恒成立,
恒成立,(2)可得
 ,
, >0恒成立,化简成
>0恒成立,化简成 恒成立,得
恒成立,得 .
.点评:关于数列方面的命题主要有以下三个方面:(1)数列本身的有关知识,其中有等差数列、等比数列的概念、性质、通项公式及求和公式;(2)数列与其他知识结合,其中有数列与函数、方程、不等式、三角、几何的结合以及探索性问题

练习册系列答案
相关题目
 是一个等差数列,且
是一个等差数列,且 ,
, .
. ; (Ⅱ)求
; (Ⅱ)求 的前
的前 项和
项和 ,则
,则 =
= 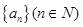 满足
满足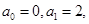 且对一切
且对一切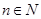 ,有
,有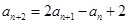
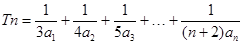 ,求
,求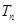 的取值范围.
的取值范围.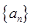 的前n项和为
的前n项和为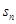 ,满足
,满足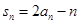
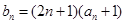 ,求数列
,求数列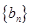 的前n项和
的前n项和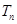 。
。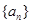 的首项
的首项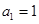 ,公差
,公差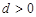 .且
.且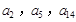 分别是等比数列
分别是等比数列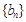 的
的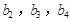 .
. 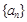 与
与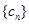 对任意自然数
对任意自然数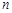 均有
均有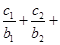 …
…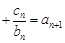 成立,求
成立,求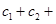 …
…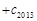 的值.
的值. 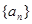 的前
的前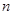 项和为
项和为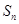 ,且
,且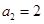 ,
,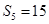 ,数列
,数列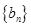 满足:
满足: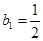 ,
,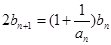 ,
,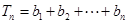 ,
,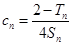 ,证明:
,证明:
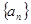 中,
中,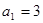 ,其前
,其前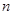 项和为
项和为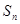 ,等比数列
,等比数列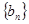 的各项均为正数,
的各项均为正数,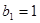 ,公比为
,公比为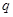 ,且
,且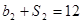 ,
, 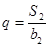 .
.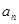 与
与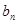 ;
;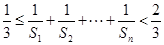 .
.