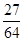题目内容
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜3次,每次相互独立;
②每次竞猜时,先由甲写出一个数字,记为a,再由乙猜甲写的数字,记为b,已知a,b∈{0,1,2,3,4,5},若|a-b|≤1,则本次竞猜成功;
③在3次竞猜中,至少有2次竞猜成功,则两人获奖.
求甲乙两人玩此游戏获奖的概率.
①连续竞猜3次,每次相互独立;
②每次竞猜时,先由甲写出一个数字,记为a,再由乙猜甲写的数字,记为b,已知a,b∈{0,1,2,3,4,5},若|a-b|≤1,则本次竞猜成功;
③在3次竞猜中,至少有2次竞猜成功,则两人获奖.
求甲乙两人玩此游戏获奖的概率.
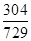
由题意基本事件的总数为 ×
× =36(个),记事件A为“甲乙两人一次竞猜成功”,若|a-b|=0,则共有6种竞猜成功;若|a-b|=1,a=1,2,3,4时,b分别有2个值;而a=0或5时,b只有一种取值.
=36(个),记事件A为“甲乙两人一次竞猜成功”,若|a-b|=0,则共有6种竞猜成功;若|a-b|=1,a=1,2,3,4时,b分别有2个值;而a=0或5时,b只有一种取值.
利用古典概型的概率计算公式即可得出P(A)=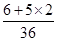 =
=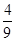 .
.
设随机变量X表示在3次竞猜中竞猜成功的次数,则甲、乙两人获奖的概率P(X≥2)=1-P(X=0)-P(X=1)=1- ×
×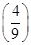 0
0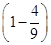 3-
3-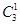
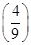 1
1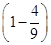 2=
2=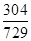 .
.
 ×
× =36(个),记事件A为“甲乙两人一次竞猜成功”,若|a-b|=0,则共有6种竞猜成功;若|a-b|=1,a=1,2,3,4时,b分别有2个值;而a=0或5时,b只有一种取值.
=36(个),记事件A为“甲乙两人一次竞猜成功”,若|a-b|=0,则共有6种竞猜成功;若|a-b|=1,a=1,2,3,4时,b分别有2个值;而a=0或5时,b只有一种取值.利用古典概型的概率计算公式即可得出P(A)=
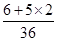 =
=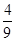 .
.设随机变量X表示在3次竞猜中竞猜成功的次数,则甲、乙两人获奖的概率P(X≥2)=1-P(X=0)-P(X=1)=1-
 ×
×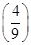 0
0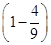 3-
3-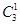
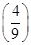 1
1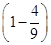 2=
2=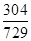 .
.
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
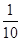

 (单位:万元),求
(单位:万元),求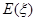 ;
; 22℃
22℃ ℃
℃

 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.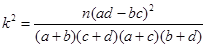



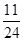


 的概率是( ).
的概率是( ).



 .
. 则射击次数为3的概率为 ( ).
则射击次数为3的概率为 ( ).