题目内容
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
 .
.(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
(1)n=2(2) 1-

(1)由题意可得 =
= ,解得n=2.
,解得n=2.
(2)①由于是不放回抽取,事件A只有两种情况:第一次取0号球,第二次取2号球;第一次取2号球,第二次取0号球.所以P(A)= .
.
②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立”.
(x,y)可以看成平面中的点,则全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域B={(x,y)|x2+y2>4,(x,y)∈Ω},所以P(B)= =1-
=1- .
.
 =
= ,解得n=2.
,解得n=2.(2)①由于是不放回抽取,事件A只有两种情况:第一次取0号球,第二次取2号球;第一次取2号球,第二次取0号球.所以P(A)=
 .
.②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立”.
(x,y)可以看成平面中的点,则全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域B={(x,y)|x2+y2>4,(x,y)∈Ω},所以P(B)=
 =1-
=1- .
.
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.


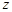





 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率.



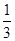 .那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.



 、
、 、
、 ,则有人能够解决这个问题的概率为
,则有人能够解决这个问题的概率为

