题目内容
4.试判断函数f(x)=$\frac{1}{x}$在区间(-∞,0)上的单调性并证明你的结论.分析 函数f(x)=$\frac{1}{x}$在区间(-∞,0)上的单调递减.利用单调性的证明方法即可得出.
解答 解:函数f(x)=$\frac{1}{x}$在区间(-∞,0)上的单调递减.证明如下:
?x1<x2<0,
则f(x1)-f(x2)=$\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}$=$\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}$.
∵x1<x2<0,∴x2-x1>0,x1x2>0.
∴f(x1)-f(x2)>0.
∴f(x1)>f(x2).
∴函数f(x)=$\frac{1}{x}$在区间(-∞,0)上的单调递减.
点评 本题考查了单调性的证明方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
16.已知$\overrightarrow{a}$,$\overrightarrow{b}$是平面内互不相等的两个非零向量,且|$\overrightarrow{a}$|=1,$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°,则|$\overrightarrow{b}$|的取值范围是( )
| A. | (0,$\sqrt{3}$] | B. | [1,$\sqrt{3}$] | C. | (0,2] | D. | [$\sqrt{3}$,2] |
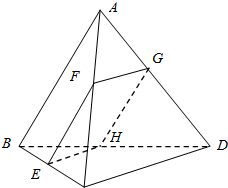 如图所示,在四面体ABCD中,截面EFGH平行于对于棱AB和CD,试问截面在什么位置时其截面面积最大?
如图所示,在四面体ABCD中,截面EFGH平行于对于棱AB和CD,试问截面在什么位置时其截面面积最大?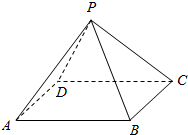 如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.
如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.