题目内容

1．已知函数f（x）=$\frac{{2}^{x}}{1+{2}^{x}}$，那么f-1（$\frac{2}{3}$）=（　　）
A．-1B．1C．-2D．2

分析 直接利用反函数的定义列出方程求解即可．

解答 解：函数f（x）=$\frac{{2}^{x}}{1+{2}^{x}}$，那么$\frac{2}{3}$=$\frac{{2}^{x}}{1+{2}^{x}}$，解得x=1，
∴f-1（$\frac{2}{3}$）=1．
故选：B．

点评 本题考查反函数的应用，是基础题．

练习册系列答案
相关题目
11．求函数f（x）=$（1+x）^{\frac{x}{tan（x-\frac{π}{4}）}}$在（0，2π）内的间断点，并判断其类型．
12．已知函数f（x）=x2+bx+c-2，若关于x的不等式-2≤f（x）≤2的解集为[x1，x2]∪[x3，x4]（x2＜x3），则W=（2x4-x3）-（2x1-x2）的最小值为4$\sqrt{3}$．
9．用斜二侧画法画一个周长为4的矩形的直观图，试求直观图面积的最大值．
16．已知$\overrightarrow{a}$，$\overrightarrow{b}$是平面内互不相等的两个非零向量，且|$\overrightarrow{a}$|=1，$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°，则|$\overrightarrow{b}$|的取值范围是（　　）
A．（0，$\sqrt{3}$]B．[1，$\sqrt{3}$]C．（0，2]D．[$\sqrt{3}$，2]
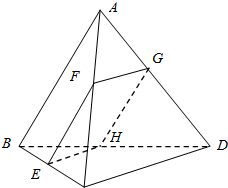6．若全称命题p：“对?x∈（1，3），x2-2ax-1≤0”为真命题，求实数a的取值范围．
13．如图所示，在四面体ABCD中，截面EFGH平行于对于棱AB和CD，试问截面在什么位置时其截面面积最大？
10．若f（cosx）=-1-2cos3x，求f（sinx）．
3．有如下几个命题：
①函数$f（x）=3sin（2x-\frac{π}{6}）+1$的一个对称轴为$x=\frac{π}{3}$；
②已知点A（2，-3），B（-3，-2），直线l：mx+y-m-1=0与线段AB相交，则直线l的斜率的范围是$[{-4，\frac{3}{4}}]$；
③若实数a+b=2，a，b为正数，则$\frac{1}{a}+\frac{4}{b}$的最小值为$\frac{9}{2}$；
④实数x，y满足3x+4y+6=0，则x2+y2+2x+4y+5的最小值为$\frac{4}{25}$；
⑤已知数列{an}的前n项和${S_n}={n^2}+3n-1$，则an=2n+1．
其中，所有正确的命题是①③．（写出所有正确命题的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网