题目内容
8．若α为第二象限角，则k•180°+α（k∈Z）的终边所在的象限是（ ）| A． | 第一象限 | B． | 第一、二象限 | C． | 第一、三象限 | D． | 第二、四象限 |
分析 由θ所在的象限，分k为偶数和奇数求得β=180°k+θ（k为整数）所在的象限．
解答 解：∵α为第二象限角，
则当k为偶数时，k•180°+α（k∈Z）是第二象限角；
当k为奇数时，k•180°+α（k为整数）是第四象限角．
故选：D．
点评 本题考查了象限角和轴线角，是基础题．
练习册系列答案
相关题目
16．已知$\overrightarrow{a}$，$\overrightarrow{b}$是平面内互不相等的两个非零向量，且|$\overrightarrow{a}$|=1，$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°，则|$\overrightarrow{b}$|的取值范围是（ ）
| A． | （0，$\sqrt{3}$] | B． | [1，$\sqrt{3}$] | C． | （0，2] | D． | [$\sqrt{3}$，2] |
3．若log${\;}_{（{a}^{2}-3）}$$\frac{1}{4}$＜log${\;}_{（{a}^{2}-3）}$$\frac{1}{3}$，则实数a的取值范围为（ ）
| A． | （-2，2） | B． | （-$\sqrt{3}$，2） | C． | （-∞，-2）∪（2，+∞） | D． | （-$\sqrt{3}$，$\sqrt{3}$） |
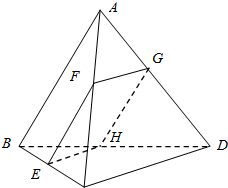如图所示，在四面体ABCD中，截面EFGH平行于对于棱AB和CD，试问截面在什么位置时其截面面积最大？