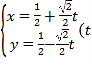题目内容
【题目】已知椭圆
的两焦点分别为
，其短半轴长为
.
（1）求椭圆的方程；
（2）设不经过点
的直线
与椭圆相交于两点
.若直线
与
的斜率之和为，求实数
的值.
【答案】(1) 
；(2)3.
【解析】
（1）根据题干条件得到a,b,c进而得到椭圆方程；（2）联立直线和椭圆方程得到二次方程，kHM+kHN
，代入韦达定理,整理可得到结果.
（1）椭圆
的两焦点分别为
，c=
, 短半轴长为
,b=1,
,故得到曲线C的方程为：；
（2）设M（x1，y1），N（x2，y2），
由
，消去y得，
37x2+36tx+9（t2﹣1）＝0，
由△＝（36t）2﹣4×37×9（t2﹣1）＞0，
可得﹣
，
又直线y＝2x+t不经过点H（0，1），
且直线HM与HN的斜率存在，
∴t≠±1，
又
，，
∴kHM+kHN
＝
，
解得t＝3，
故t的值为3.
【题目】某校有教师400人，对他们进行年龄状况和学历的调查，其结果如下：
学历 | 35岁以下 | 35-55岁 | 55岁及以上 |
本科 |
| 60 | 40 |
硕士 | 80 | 40 |
|
(1)若随机抽取一人，年龄是35岁以下的概率为
，求
；
(2)在35-55岁年龄段的教师中，按学历状况用分层抽样的方法，抽取一个样本容量为5的样本，然后在这5名教师中任选2人，求两人中至多有1人的学历为本科的概率.
【题目】某校高三文科
名学生参加了
月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从名学生中抽取
名学生的成绩进行统计分析，抽出的名学生的地理、历史成绩如下表：
地理 历史 | [80,100] | [60,80） | [40,60） |
[80,100] | 8 | m | 9 |
[60,80） | 9 | n | 9 |
[40,60） | 8 | 15 | 7 |
若历史成绩在[80,100]区间的占30%，
（1）求
的值；
（2）请根据上面抽出的名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：
[80,100] | [60,80） | [40,60） | |
地理 | |||
历史 |
根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定.
