题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为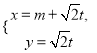 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 经过曲线
经过曲线![]() 的左焦点
的左焦点![]() .
.
(1)求直线![]() 的普通方程;
的普通方程;
(2)设曲线![]() 的内接矩形的周长为
的内接矩形的周长为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)椭圆
(2)椭圆![]() 的内接矩形的周长取得最大值
的内接矩形的周长取得最大值![]() .
.
【解析】试题分析:(1)由直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数)消去参数t,得到直线
为参数)消去参数t,得到直线![]() 的普通方程;(2)设椭圆
的普通方程;(2)设椭圆![]() 的内接矩形在第一象限的顶点为
的内接矩形在第一象限的顶点为![]() (
(![]() ),则周长为
),则周长为![]() ,利用辅助角公式“化一”求最值即可.
,利用辅助角公式“化一”求最值即可.
试题解析:
(1)因为曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,
,
将![]() ,
, ![]() 代入上式并化简得
代入上式并化简得![]() ,
,
所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,于是
,于是![]() ,
, ![]() ,
,
直线![]() 的普通方程为
的普通方程为![]() ,将
,将![]() 代入直线方程得
代入直线方程得![]() ,
,
所以直线![]() 的普通方程为
的普通方程为![]() .
.
(2)设椭圆![]() 的内接矩形在第一象限的顶点为
的内接矩形在第一象限的顶点为![]() (
(![]() ),
),
所以椭圆![]() 的内接矩形的周长为
的内接矩形的周长为![]() (其中
(其中![]() ),
),
此时椭圆![]() 的内接矩形的周长取得最大值
的内接矩形的周长取得最大值![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.