题目内容
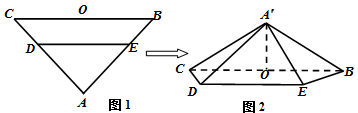
在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.
(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)在(1)的条件下,求异面直线AE与CD所成角的余弦值;
(3)求平面PAB与平面PCD所成的锐二面角的正切值.

(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)在(1)的条件下,求异面直线AE与CD所成角的余弦值;
(3)求平面PAB与平面PCD所成的锐二面角的正切值.

解法一:(1)∵∠BAD=90°,∴BA⊥AD
∵PA⊥底面ABCD,BA⊥PA.又∵PA∩AD=A,BA⊥PA.又∵PA∩AD=A,
∴BA⊥平面PAD.
∵PD?平面PAD.
∴PD⊥BA.又∵PD⊥AE,且BA∩AE=A,
∴PD⊥平面BAE
∴PD⊥BE,即BE⊥PD.(4分)
(2)过点E作EM∥CD交PC于M,连接AM,则AE与ME所成角即为AE与CD所成角

∵PA⊥底面ABCD,且PD与底面ABCD成30°角.
∴∠PDA=30°.
∴在Rt△PAD中,∠PAD=90°,∠PDA=30°,AD=2a
∴PA=
a,PD=
a.
∴AE=
=
=a.
∵PE=
=
=
a,CD=
a.
∴ME=
=
=
a.
连接AC
∵在△ACD中AD=2a,AC=
a,CD=
a,
AD2=AC2+CD2
∴∠ACD=90°,∴CD⊥AC,∴ME⊥AC
又∵PA⊥底面ABCD,
∴PA⊥CD,∴ME⊥PA.
∴ME⊥平面PAC.∵MA?平面PAC,
∵ME⊥AM.
∴在Rt△AME中,cos∠MEA=
=
.
∴异面直线AE与CD所成角的余弦值为
(9分)
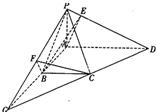
(3)延长AB与DC相交于G点,连PG,则面PAB
与面PCD的交线为PG,易知CB⊥平面PAB,过B作BF⊥PG于F点,连CF,则CF⊥PG,
∴∠CFB为二面角C-PG-A的平面角,
∵CB∥
AD,
∴GB=AB=a,∠PDA=30°,PA=
a,AG=2a.
∴∠PGA=30°,
∴BF=
GB=
,tanBFC=
=2,
∴平面PAB与平面PCD所成的二面角的正切值为2.(14分)
解法二:(1)如图建立空间直角坐标系,
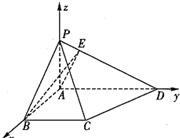
则A(0,0,0),B(a,0,0),E(0,
a,
a),C(a,a,0),
D(0,2a,0),P(0,0,
a)
∴
=(-a,
a,
a),
=(0,2a,-
a),
∴
•
=(-a)×0+
a•2a+
a•(-
)=0,
∴BE⊥PD(4分)
(2)由(1)知,
=(0,
a,
a),
=(-a,a,0)设
与
所成角为θ
则cosθ=
=
=
,
∴异面直线AE与CD所成角的余统值为
.(9分)
(3)易知,CB⊥AB,CB⊥PA,
则CB⊥平面PAB.,∴
是平面PAB的法向量.∴
∵PA⊥底面ABCD,BA⊥PA.又∵PA∩AD=A,BA⊥PA.又∵PA∩AD=A,
∴BA⊥平面PAD.
∵PD?平面PAD.
∴PD⊥BA.又∵PD⊥AE,且BA∩AE=A,
∴PD⊥平面BAE
∴PD⊥BE,即BE⊥PD.(4分)
(2)过点E作EM∥CD交PC于M,连接AM,则AE与ME所成角即为AE与CD所成角

∵PA⊥底面ABCD,且PD与底面ABCD成30°角.
∴∠PDA=30°.
∴在Rt△PAD中,∠PAD=90°,∠PDA=30°,AD=2a
∴PA=
2
| ||
| 3 |
4
| ||
| 3 |
∴AE=
| PA•AD |
| PD |
| ||||
|
∵PE=
| PA2 |
| PD |
(
| ||||
|
| ||
| 3 |
| 2 |
∴ME=
| CD•PE |
| PD |
| ||||||
|
| ||
| 4 |
连接AC
∵在△ACD中AD=2a,AC=
| 2 |
| 2 |
AD2=AC2+CD2
∴∠ACD=90°,∴CD⊥AC,∴ME⊥AC
又∵PA⊥底面ABCD,
∴PA⊥CD,∴ME⊥PA.
∴ME⊥平面PAC.∵MA?平面PAC,
∵ME⊥AM.
∴在Rt△AME中,cos∠MEA=
| ME |
| AE |
| ||
| 4 |

∴异面直线AE与CD所成角的余弦值为
| ||
| 4 |
(9分)
(3)延长AB与DC相交于G点,连PG,则面PAB
与面PCD的交线为PG,易知CB⊥平面PAB,过B作BF⊥PG于F点,连CF,则CF⊥PG,
∴∠CFB为二面角C-PG-A的平面角,
∵CB∥
| 1 |
| 2 |
∴GB=AB=a,∠PDA=30°,PA=
2
| ||
| 3 |
∴∠PGA=30°,
∴BF=
| 1 |
| 2 |
| a |
| 2 |
| a | ||
|
∴平面PAB与平面PCD所成的二面角的正切值为2.(14分)
解法二:(1)如图建立空间直角坐标系,

则A(0,0,0),B(a,0,0),E(0,
| 1 |
| 2 |
| ||
| 2 |
D(0,2a,0),P(0,0,
2
| ||
| 3 |
∴
| BE |
| 1 |
| 2 |
| ||
| 2 |
| PD |
2
| ||
| 2 |
∴
| BE |
| PD |
| 1 |
| 2 |
| ||
| 2 |
2
| ||
| 2 |
∴BE⊥PD(4分)
(2)由(1)知,
| AE |
| 1 |
| 2 |
| ||
| 2 |
| CD |
| AE |
| CD |
则cosθ=
| ||||
|
|
0×(-a)+
| ||||||||||
|
| ||
| 4 |
∴异面直线AE与CD所成角的余统值为
| ||
| 4 |
(3)易知,CB⊥AB,CB⊥PA,
则CB⊥平面PAB.,∴
| BC |

练习册系列答案
相关题目
|