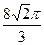题目内容
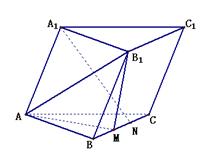
如图,在组合体中, 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
, ,点
,点 且
且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)求面 与面
与面 所成的角的正切值;
所成的角的正切值;
(Ⅲ)若 ,当
,当 为何值时,
为何值时, .
.

 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
, ,点
,点 且
且 .
.(Ⅰ)证明:
 ;
;(Ⅱ)求面
 与面
与面 所成的角的正切值;
所成的角的正切值;(Ⅲ)若
 ,当
,当 为何值时,
为何值时, .
.
(1)略(2)3(3)2
(Ⅰ)证明:
因为 ,
,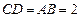 ,所以
,所以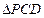 为等腰直角三角形,所以
为等腰直角三角形,所以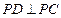 . ……1分
. ……1分
因为 是一个长方体,所以
是一个长方体,所以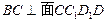 ,而
,而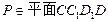 ,所以
,所以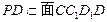 ,所以
,所以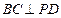 . …3分
. …3分
因为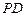 垂直于平面
垂直于平面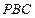 内的两条相交直线
内的两条相交直线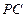 和
和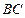 ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得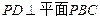 .…4分
.…4分
(Ⅱ)解:过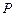 点在平面
点在平面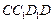 作
作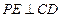 于
于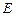 ,取
,取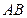 的中点F连接
的中点F连接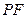 …5分
…5分
则所以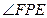 就是所求二面角的平面角.……6分
就是所求二面角的平面角.……6分

因为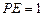 ,
,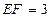 ,,所以
,,所以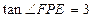 . …8分
. …8分
(Ⅲ)解:当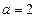 时,
时,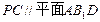 . …9分
. …9分
当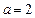 时,四边形
时,四边形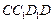 是一个正方形,所以
是一个正方形,所以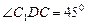 ,而
,而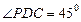 ,所以
,所以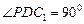 ,所以
,所以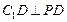 . …10分
. …10分
而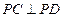 ,
,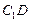 与
与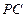 在同一个平面内,所以
在同一个平面内,所以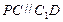 . …11分
. …11分
而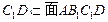 ,所以
,所以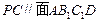 ,所以
,所以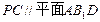 。…12分
。…12分
因为
 ,
,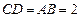 ,所以
,所以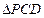 为等腰直角三角形,所以
为等腰直角三角形,所以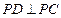 . ……1分
. ……1分因为
 是一个长方体,所以
是一个长方体,所以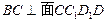 ,而
,而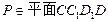 ,所以
,所以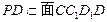 ,所以
,所以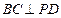 . …3分
. …3分因为
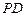 垂直于平面
垂直于平面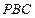 内的两条相交直线
内的两条相交直线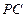 和
和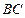 ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得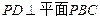 .…4分
.…4分(Ⅱ)解:过
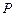 点在平面
点在平面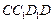 作
作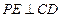 于
于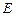 ,取
,取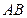 的中点F连接
的中点F连接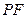 …5分
…5分则所以
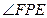 就是所求二面角的平面角.……6分
就是所求二面角的平面角.……6分
因为
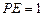 ,
,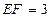 ,,所以
,,所以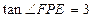 . …8分
. …8分(Ⅲ)解:当
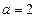 时,
时,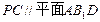 . …9分
. …9分当
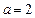 时,四边形
时,四边形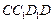 是一个正方形,所以
是一个正方形,所以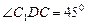 ,而
,而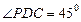 ,所以
,所以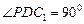 ,所以
,所以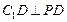 . …10分
. …10分而
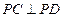 ,
,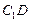 与
与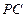 在同一个平面内,所以
在同一个平面内,所以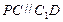 . …11分
. …11分而
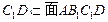 ,所以
,所以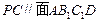 ,所以
,所以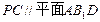 。…12分
。…12分
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
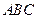 ,
,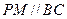 ,PA = PC,
,PA = PC,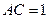 ,
,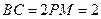 ,
,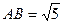 ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为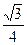 .
.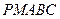 的体积V.
的体积V.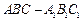 中,侧面
中,侧面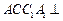
 平面
平面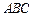 ,
,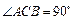 .
.
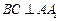 ;
;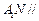 平面
平面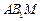 .
.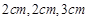 ,若该长方体的各顶点都在球
,若该长方体的各顶点都在球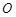 的表面上,则球
的表面上,则球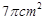
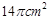
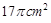

 的中心,点E为面
的中心,点E为面 的中心,点F为
的中心,点F为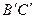 的中点,则空间四边形
的中点,则空间四边形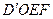 在该正方体的面上的正投影的所有可能的图形的序号是_______.
在该正方体的面上的正投影的所有可能的图形的序号是_______.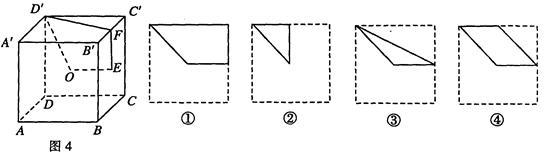
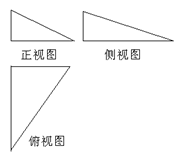
 ,球面上有
,球面上有 三点,
三点,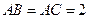 ,
,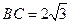 ,
, 为球心,则直线
为球心,则直线 与平面
与平面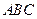 所成的角的正切值为 .
所成的角的正切值为 .
 的平面去截该球,所得截面面积为
的平面去截该球,所得截面面积为 ,则该球的体积( )
,则该球的体积( )