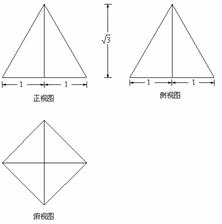
题目内容
(本小题满分14分)
在斜三棱柱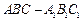 中,侧面
中,侧面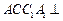
 平面
平面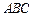 ,
,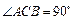 .
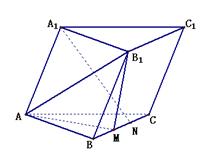
.
(I)求证: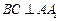 ;
;
(II)若M,N是棱BC上的两个三等分点,
求证: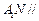 平面
平面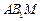 .
.
在斜三棱柱
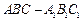 中,侧面
中,侧面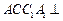
 平面
平面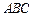 ,
,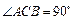 .
.
(I)求证:
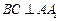 ;
;(II)若M,N是棱BC上的两个三等分点,
求证:
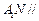 平面
平面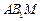 .
.略
(Ⅰ) 因为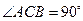 ,所以
,所以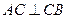 , ……… 1分
, ……… 1分
又侧面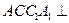 平面
平面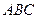 ,且平面
,且平面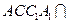 平面
平面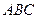 =AC,…………3分
=AC,…………3分
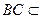 平
平 面
面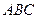 ,所以
,所以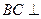 平面
平面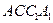 , ………… 5分
, ………… 5分
又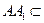 平面
平面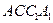 ,所以
,所以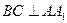 . ………… 7分
. ………… 7分
(II)连接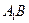 ,交
,交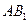 于O点,连接MO, ………… 9分
于O点,连接MO, ………… 9分
在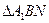 中,O,M分别为
中,O,M分别为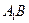 ,BN的中点, 所以OM //
,BN的中点, 所以OM //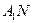 ………… 11分
………… 11分
又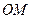
 平面
平面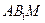 ,
,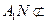 平面
平面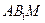 , ………… 13分
, ………… 13分
所以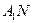 //平面
//平面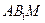 . ………… 14分
. ………… 14分
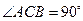 ,所以
,所以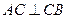 , ……… 1分
, ……… 1分又侧面
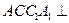 平面
平面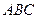 ,且平面
,且平面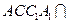 平面
平面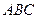 =AC,…………3分
=AC,…………3分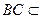 平
平 面
面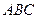 ,所以
,所以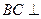 平面
平面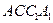 , ………… 5分
, ………… 5分又
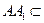 平面
平面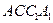 ,所以
,所以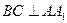 . ………… 7分
. ………… 7分(II)连接
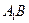 ,交
,交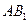 于O点,连接MO, ………… 9分
于O点,连接MO, ………… 9分在
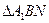 中,O,M分别为
中,O,M分别为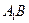 ,BN的中点, 所以OM //
,BN的中点, 所以OM //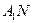 ………… 11分
………… 11分又
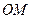
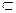 平面
平面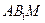 ,
,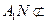 平面
平面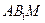 , ………… 13分
, ………… 13分所以
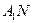 //平面
//平面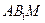 . ………… 14分
. ………… 14分
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
, ,点
,点 且
且 .
. ;
; 与面
与面 所成的角的正切值;
所成的角的正切值; ,当
,当 为何值时,
为何值时, .
.
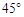 圈上有两个点A、B,A在西经
圈上有两个点A、B,A在西经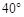 ,B在东经
,B在东经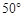 ,则A、B两点间的球面距离为( )
,则A、B两点间的球面距离为( )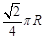 B.
B.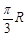 C.
C.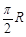 D.
D.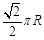
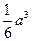
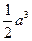
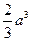
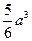

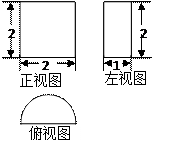
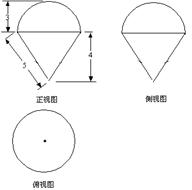

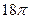
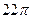
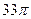
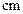 )如图
)如图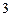 所示,则此几何体的表面积是
所示,则此几何体的表面积是 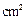 .
.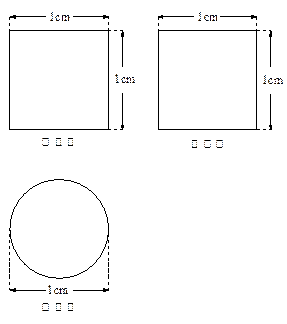

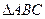 中,若
中,若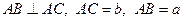 ,则
,则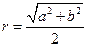 ,将此结论拓展到空间,可得出的正确结论是:在四面体
,将此结论拓展到空间,可得出的正确结论是:在四面体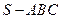 中,若
中,若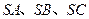 两两垂直,
两两垂直,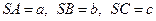 ,则四面体
,则四面体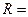 .
. 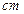 )如图所示,
)如图所示,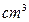 .
.