题目内容
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| A.(0,2) | B.[0,2] |
| C.(2,+∞) | D.[2,+∞) |
C
∵x2=8y,
∴焦点F的坐标为(0,2),准线方程为y=-2.
由抛物线的定义知|MF|=y0+2.以F为圆心、|FM|为半径的圆的标准方程为x2+(y-2)2=(y0+2)2.
由于以F为圆心、|FM|为半径的圆与准线相交,又圆心F到准线的距离为4,故4<y0+2,∴y0>2.故选C.
∴焦点F的坐标为(0,2),准线方程为y=-2.
由抛物线的定义知|MF|=y0+2.以F为圆心、|FM|为半径的圆的标准方程为x2+(y-2)2=(y0+2)2.
由于以F为圆心、|FM|为半径的圆与准线相交,又圆心F到准线的距离为4,故4<y0+2,∴y0>2.故选C.

练习册系列答案
相关题目
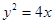 的焦点作直线
的焦点作直线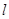 交抛物线于A、B两点,若线段AB中点的横坐标为3,则
交抛物线于A、B两点,若线段AB中点的横坐标为3,则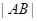 等于 .
等于 .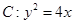 的焦点
的焦点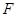 作直线
作直线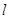 交抛物线
交抛物线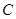 于
于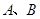 两点,若A到抛物线的准线的距离为4,则
两点,若A到抛物线的准线的距离为4,则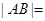 .
.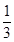 (B)
(B) 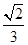 (C)
(C) 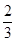 (D)
(D) 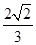
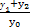 的值为 .
的值为 .
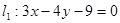 和直线
和直线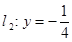 ,抛物线
,抛物线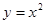 上一动点
上一动点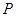 到直线
到直线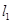 和直线
和直线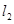 的距离之和的最小值是 。
的距离之和的最小值是 。