题目内容
【题目】某大学为调研学生在
， 
两家餐厅用餐的满意度，从在
， 
两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分.
整理评分数据，将分数以10为组距分成6组： 
， 
， 
， 
， 
， 
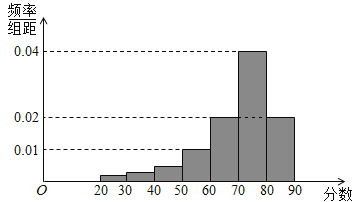
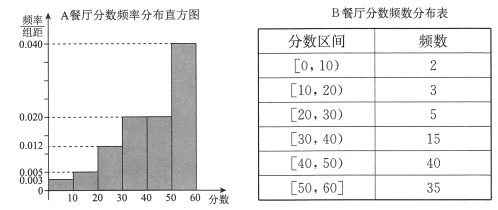
，得到
餐厅分数的频率分布直方图，和
餐厅分数的频数分布表：
（Ⅰ）在抽样的100人中，求对
餐厅评分低于30的人数；
（Ⅱ）从对
餐厅评分在
范围内的人中随机选出2人，求2人中恰有1人评分在
范围内的概率；
（Ⅲ）如果从
， 
两家餐厅中选择一家用餐，你会选择哪一家？说明理由.
【答案】（I）
人；（II）
；（III）详见解析.
【解析】试题分析：（Ⅰ）计算前三个小矩形面积和即可得结果；（Ⅱ）列举出所有从这
人中随机选出
人的所有情况共
种，符合条件的有
种，有古典概型概率公式可得结果；（III）比较得分低于
分的比例即可得结果.
试题解析：（Ⅰ）由
餐厅分数的频率分布直方图，得
对
餐厅评分低于
的频率为
，
所以，对
餐厅评分低于
的人数为
.
（Ⅱ）对
餐厅评分在
范围内的有
人，设为
；
对
餐厅评分在
范围内的有
人，设为
.
从这
人中随机选出
人的选法为：
， 
， 
， 
， 
， 
， 
， 
， 
， 
共
种.
其中，恰有
人评分在
范围内的选法为： 
， 
， 
， 
， 
， 
.共6种.
故
人中恰有
人评分在
范围内的概率为
.
（Ⅲ）从两个餐厅得分低于
分的数所占的比例来看：
由（Ⅰ）得，抽样的
人中， 
餐厅评分低于
的人数为
，
所以， 
餐厅得分低于
分的人数所占的比例为
.
餐厅评分低于
的人数为
，
所以， 
餐厅得分低于
分的人数所占的比例为
.
所以会选择
餐厅用餐.
练习册系列答案
相关题目
