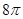题目内容
如图,在直三棱柱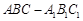 中,
中,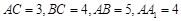 ,
,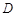 为
为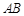 的中点.
的中点.
(I)求证: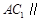 平面
平面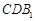 ;
;
(II)求平面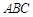 和平面
和平面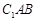 夹角的余弦值.
夹角的余弦值.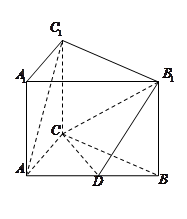
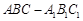 中,
中,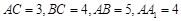 ,
,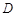 为
为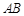 的中点.
的中点.(I)求证:
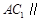 平面
平面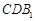 ;
;(II)求平面
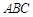 和平面
和平面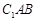 夹角的余弦值.
夹角的余弦值.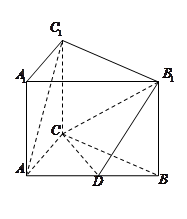
(1)证明略 (2)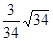 .
.
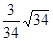 .
.(1)关键在平面B1CD内找到与AC1平行的直线,涉及到中点想到构造中位线解决.本题连接BC1交B1C于O点连接OD,则证明OD//AC1即可.
(2)先做出其平面角,过C作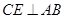 于E点,连接C1E,
于E点,连接C1E,
则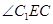 就是二面角C-AB-C1的平面角,然后解三角形即可
就是二面角C-AB-C1的平面角,然后解三角形即可
(1)证明:设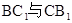 交于点O,则O为
交于点O,则O为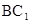 的中点.
的中点.
在△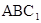 中,连接OD,D,O分别为AB,
中,连接OD,D,O分别为AB,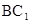 的中点,故OD为△
的中点,故OD为△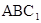 的中位线,
的中位线,
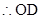 ∥
∥ ,又
,又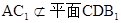 ,
,
 ,
,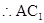 ∥平面
∥平面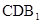 .……6分
.……6分
(2):过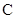 作
作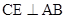 于
于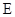 ,连接
,连接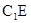 .由
.由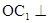 底面
底面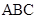 可得
可得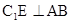 .
.
故∠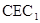 为二面角
为二面角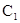 --
--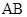 --
--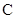 的平面角.在△
的平面角.在△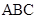 中,
中,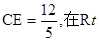 △
△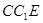
中,tan∠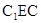 =
=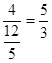 ,
, 二面角
二面角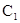 --
--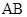 --
--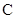 的余弦值为
的余弦值为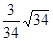 .
.
(2)先做出其平面角,过C作
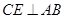 于E点,连接C1E,
于E点,连接C1E,则
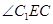 就是二面角C-AB-C1的平面角,然后解三角形即可
就是二面角C-AB-C1的平面角,然后解三角形即可(1)证明:设
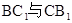 交于点O,则O为
交于点O,则O为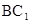 的中点.
的中点.在△
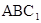 中,连接OD,D,O分别为AB,
中,连接OD,D,O分别为AB,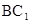 的中点,故OD为△
的中点,故OD为△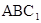 的中位线,
的中位线,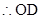 ∥
∥ ,又
,又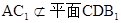 ,
, ,
,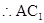 ∥平面
∥平面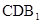 .……6分
.……6分(2):过
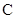 作
作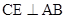 于
于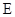 ,连接
,连接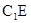 .由
.由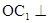 底面
底面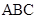 可得
可得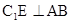 .
.故∠
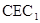 为二面角
为二面角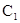 --
--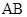 --
--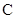 的平面角.在△
的平面角.在△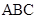 中,
中,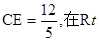 △
△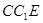
中,tan∠
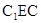 =
=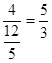 ,
, 二面角
二面角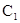 --
--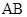 --
--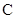 的余弦值为
的余弦值为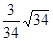 .
.
练习册系列答案
相关题目
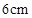 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.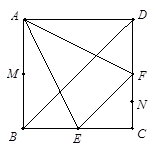
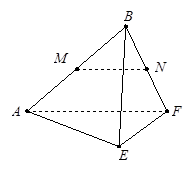
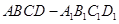 中,底面
中,底面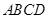 是边长为
是边长为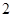 的正方形,
的正方形,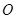 为
为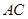 与
与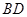 的交点,
的交点,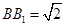 ,
,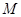 是线段
是线段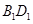 的中点.
的中点.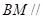 平面
平面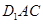 ;
;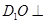 平面
平面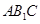 ;
;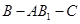 的大小.
的大小. 中,
中,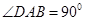 ,
,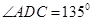 ,
,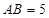 ,
,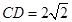 ,
,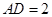 ,
,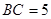 ,求四边形
,求四边形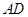 旋转一周所成几何体的表面积及体积
旋转一周所成几何体的表面积及体积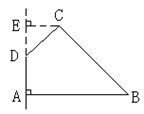
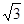 、
、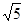 、
、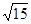 ,则它的外接球的表面积为
,则它的外接球的表面积为