题目内容
3.在△ABC中,角A,B,C的所对的边分别为a,b,c,且a2+b2=ab+c2.(Ⅰ) 求tan(C-$\frac{π}{4}$)的值;
(Ⅱ) 若c=$\sqrt{3}$,求S△ABC的最大值.
分析 (Ⅰ) 利用余弦定理表示出cosC,将已知等式变形后代入求出cosC的值,确定出C的度数,代入tan(C-$\frac{π}{4}$)计算即可求出值;
(Ⅱ)把c的值代入已知等式变形,利用基本不等式求出ab的最大值,再由sinC的值,即可求出三角形ABC面积的最大值.
解答 解:(Ⅰ)∵a2+b2=ab+c2,a2+b2-c2=ab,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
∵C为△ABC内角,
∴C=$\frac{π}{3}$,
则tan(C-$\frac{π}{4}$)=tan($\frac{π}{3}$-$\frac{π}{4}$)=$\frac{\sqrt{3}-1}{1+\sqrt{3}}$=2-$\sqrt{3}$;
(Ⅱ)由ab+3=a2+b2≥2ab,得ab≤3,
∵S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab,
∴S△ABC≤$\frac{3\sqrt{3}}{4}$,
当且仅当a=b=$\sqrt{3}$时“=”成立,
则S△ABC的最大值是$\frac{{3\sqrt{3}}}{4}$.
点评 此题考查了余弦定理,三角形面积公式,以及基本不等式的运用,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
13.直角三角形ABC中,A为直角,AB=1,BC=2,若点AM是BC边上的高线,点P在△ABC 内部或边界上运动,则$\overrightarrow{AM}$•$\overrightarrow{BP}$的范围是( )
| A. | [-$\frac{\sqrt{3}}{2}$,0] | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{\sqrt{3}}{4}$,0] | D. | [-3,0] |
11.已知直线y=kx+2与圆(x+2)2+(y-1)2=4相交于M,N两点,若|MN|≥2$\sqrt{3}$,则k的取值范围是( )
| A. | [$\frac{1}{2}$,$\frac{4}{3}$] | B. | [0,$\frac{1}{2}$] | C. | (-∞,0]∪[$\frac{4}{3}$,+∞) | D. | [0,$\frac{4}{3}$] |
18.要得到函数f(x)=sin(2x+$\frac{π}{4}$)的图象,只需将函数g(x)=sin2x的图象( )
| A. | 向左平移$\frac{π}{8}$个单位长度 | B. | 向右平移$\frac{π}{8}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
8.若集合U={2,0,1,3,4,5},集合A={0,3,4,2},B={0,1,2,3,4},则∁U(A∩B)=( )
| A. | {0,3,4,2} | B. | {0,2} | C. | {1,5} | D. | {2,0,1,5} |
13.已知命题p:函数y=f(x)在区间[a,b]上单调递增,命题q:函数y=f(x)单调递增区间为[a,b],则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
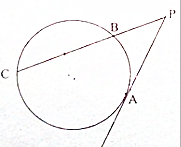 如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.
如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.