Question

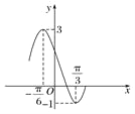
【题目】已知函数g(x)＝Acos(ωx＋φ)＋B的部分图象如图所示，将函数g(x)的图象保持纵坐标不变，横坐标向右平移个单位长度后得到函数f(x)的图象．求：

(1)函数f(x)在上的值域；

(2)使f(x)≥2成立的x的取值范围．

Answer 1

【答案】(1) [0,3] (2)

【解析】

（1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得函数g（x）的解析式．再根据函数y＝Acos（ωx+φ）+B的图象的平移变换规律，可得f（x）的解析式，再根据x∈[，]，利用余弦函数的定义域和值域求得可得f（x）的值域；

（2）由f（x）≥2可得 cos（2x），故有2kπ2x2kπ，k∈z，由此求得不等式的解集．

(1)由图知B＝＝1，A＝＝2，T＝2（）＝π，

所以ω＝2，所以g(x)＝2cos(2x＋φ)＋1.

把()代入，得2cos（）＋1＝－1，

即＋φ＝π＋2kπ(k∈Z)，

所以φ＝2kπ＋ (k∈Z)．

因为|φ|<，所以φ＝，

所以g(x)＝2cos（2x+）＋1，

所以f(x)＝2cos（2x-）＋1.

因为x∈，所以2x－∈，

所以f(x)∈[0,3]，即函数f(x)在上的值域为[0,3]．

(2)因为f(x)＝2cos（2x-）＋1，

所以2cos（2x-）＋1≥2，

所以cos（2x-）≥，

所以－＋2kπ≤2x－≤＋2kπ(k∈Z)，

所以kπ≤x≤kπ＋(k∈Z)，

所以使f(x)≥2成立的x的取值范围是.