题目内容
【题目】如图为一个正方体
与一个半球
构成的组合体，半球的底面圆与该正方体的上底面
的四边相切， 与正方形的中心重合.将此组合体重新置于一个球
中(球未画出)，使该正方体的下底面
的顶点均落在球的表面上，半球与球内切，设切点为
，若正四棱锥
的表面积为
，则球的表面积为（ ）
A.
B.
C.
D.
【答案】B
【解析】
设球
，半球
的半径分别为
，然后用含
的式子表示出正方体的棱长与四棱锥
的高和四棱锥侧面的高，从而由四棱锥的表面积求出，进而建立关于
的方程，求得的值，最后利用球的表面积公式求解即可.
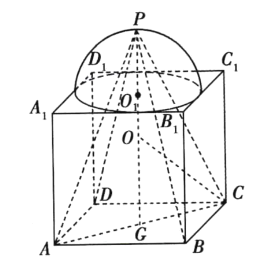
如图，
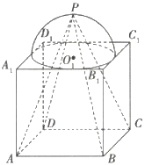
设球，半球的半径分别为， 由题意知正方体
的棱长为
，四棱锥为正四棱锥.设该正方体的底面
的中心为
，连接
，则四棱锥的高
，其各侧面的高为
.由题意得
，得
.易知球的球心在线段
上，连接
，则在
中， 
，
于是由勾股定理，得
解得
，所以球的表面积
，
故选：B.
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
