题目内容
【题目】如图,在四棱锥 ![]() 中,底面
中,底面 ![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 中点.
中点.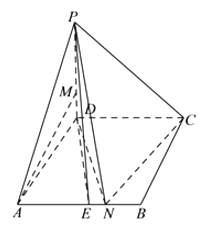
(I)求证:直线 ![]() 平面
平面 ![]() .
.
(II)求证:直线 ![]() 平面
平面 ![]() .
.
(III)在 ![]() 上是否存在一点
上是否存在一点 ![]() ,使得二面角
,使得二面角 ![]() 的大小为
的大小为 ![]() ,若存在,确定
,若存在,确定 ![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
【答案】解:证明:(I)在 ![]() 上取点
上取点 ![]() ,使
,使 ![]() ,连接
,连接 ![]() ,
, ![]() ,
,
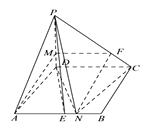
因为 ![]() ,
, ![]() ,
,
所以 ![]() ,且
,且 ![]() ,
,
因为 ![]() ,
, ![]() ,
,
所以 ![]() ,且
,且 ![]() ,
,
所以四边形 ![]() 为平行四边形,
为平行四边形,
所以 ![]() ,
,
又 ![]() 平面
平面 ![]() ,
, ![]()
![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]()
(Ⅱ)因为 ![]() 是
是 ![]() 中点,底面
中点,底面 ![]() 是菱形,
是菱形, ![]() ,
,
所以 ![]() ,
,
因为 ![]() ,
,
所以 ![]() ,
,
所以 ![]() .
.
又 ![]() 平面
平面 ![]() ,
,
所以 ![]()
又 ![]()
所以直线 ![]() 平面
平面 ![]()
(III)由(Ⅱ)可知 ![]() ,
, ![]() ,
, ![]() ,相互垂直,以
,相互垂直,以 ![]() 为原点,建立如图所示的空间直角坐标系D-xyz.
为原点,建立如图所示的空间直角坐标系D-xyz.
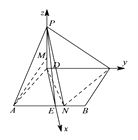
则 ![]() ,
, ![]() ,
, ![]() ,
,
假设存在点G满足条件,其坐标为 ![]()
设平面 ![]() 的一个法向量为
的一个法向量为 ![]() ,
,
由  ,得
,得 ![]() ,
,
令 ![]() ,则
,则 ![]()
同理可得平面 ![]() 的法向量
的法向量 ![]() ,
,
由题意得
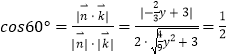 ,
,
解得 ![]()
所以点 ![]() 。
。
所以当点 ![]() 与点
与点 ![]() 重合时,二面角
重合时,二面角 ![]() 的大小为
的大小为 ![]() .
.
因此点 ![]() 为所求的点。
为所求的点。
【解析】(1)根据题意作出辅助线结合已知可得到四边形 M F N A 为平行四边形,即A M ∥ N F。再由线面平行的判定定理可得A M ∥ 平面 P N C。(2)由E是AB的中点底面ABCD是菱形, ∠ D A B = 60 °可得∠ A ED = 9 0 °进而得出 C D ⊥ D E ,再利用线面垂直的判定定理可得结论。(3)根据(2)的结论可知D P , D E , D C ,相互垂直,以 D 为原点,建立如图所示的空间直角坐标系D-xyz,然后利用平面法向量所成角的余弦值即可求得G点的位置。
【考点精析】通过灵活运用直线与平面垂直的判定和直线与平面垂直的性质,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;垂直于同一个平面的两条直线平行即可以解答此题.
