题目内容
【题目】已知数列{an},{bn}满足bn=an+1﹣an(n=1,2,3,…).
(1)若bn=10﹣n,求a16﹣a5的值;
(2)若 ![]() 且a1=1,则数列{a2n+1}中第几项最小?请说明理由;
且a1=1,则数列{a2n+1}中第几项最小?请说明理由;
(3)若cn=an+2an+1(n=1,2,3,…),求证:“数列{an}为等差数列”的充分必要条件是“数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…)”.
【答案】
(1)由bn=10﹣n,可得bn+1﹣bn=(9﹣n)﹣(10﹣n)=﹣1,故{bn}是等差数列.
所以a16﹣a5=(a16﹣a15)+(a15﹣a14)+(a14﹣a13)+…+(a6﹣a5)= ![]()
(2)a2n+3﹣a2n+1=(a2n+3﹣a2n+2)+(a2n+2﹣a2n+1)=b2n+2+b2n+1=(22n+2+231﹣2n)﹣(22n+1+232﹣2n)=22n+1﹣231﹣2n
由a2n+3<a2n+122n+1﹣231﹣2n<0n<7.5,a2n+3>a2n+122n+1﹣231﹣2n>0n>7.5,
故有a3>a5>a7>…>a15>a17<a19<a20<…,
所以数列{a2n+1}中a17最小,即第8项最小.
法二:由 ![]() ,可知a2n+1=a1+b1+b2+b3+…+b2n=
,可知a2n+1=a1+b1+b2+b3+…+b2n= 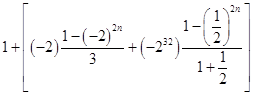 =
= ![]() (当且仅当22n+1=233﹣2n,即n=8时取等号)
(当且仅当22n+1=233﹣2n,即n=8时取等号)
所以数列{a2n+1}中的第8项最小
(3)若数列{an}为等差数列,设其公差为d,
则cn+1﹣cn=(an+1﹣an)+2(an+2﹣an+1)=d+2d=3d为常数,
所以数列{cn}为等差数列.
由bn=an+1﹣an=d(n=1,2,3,…),可知bn≤bn+1(n=1,2,3,…).
若数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…),设{cn}的公差为D,
则cn+1﹣cn=(an+1﹣an)+2(an+2﹣an+1)=bn+2bn+1=D(n=1,2,3,…),
又bn+1+2bn+2=D,故(bn+1﹣bn)+2(bn+2﹣bn+1)=D﹣D=0,
又bn+1﹣bn≥0,bn+2﹣bn+1≥0,故bn+1﹣bn=bn+2﹣bn+1=0(n=1,2,3,…),所以bn+1=bn(n=1,2,3,…),故有bn=b1,所以an+1﹣an=b1为常数.
故数列{an}为等差数列.
综上可得,“数列{an}为等差数列”的充分必要条件是“数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…)”
【解析】(1)判断{bn}是等差数列.然后化简a16﹣a5=(a16﹣a15)+(a15﹣a14)+(a14﹣a13)+…+(a6﹣a5)利用等差数列的性质求和即可.(2)利用a2n+3﹣a2n+1=22n+1﹣231﹣2n , 判断a2n+3<a2n+1 , 求出n<7.5,a2n+3>a2n+1求出n>7.5,带带数列{a2n+1}中a17最小,即第8项最小. 法二:化简![]() ,
,
求出a2n+1=a1+b1+b2+b3+…+b2n= ,利用基本不等式求出最小值得到数列{a2n+1}中的第8项最小.(3)若数列{an}为等差数列,设其公差为d,说明数列{cn}为等差数列. 由bn=an+1﹣an=d(n=1,2,3,…),推出bn≤bn+1 , 若数列{cn}为等差数列且bn≤bn+1(n=1,2,3,…),设{cn}的公差为D,转化推出bn+1=bn(n=1,2,3,…),说明数列{an}为等差数列.得到结果.
【考点精析】掌握数列的通项公式是解答本题的根本,需要知道如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 互动英语系列答案
互动英语系列答案