题目内容
【题目】已知 ![]() 为常数),
为常数), ![]() ,且当x1 , x2∈[1,4]时,总有f(x1)≤g(x2),则实数a的取值范围是 .
,且当x1 , x2∈[1,4]时,总有f(x1)≤g(x2),则实数a的取值范围是 .
【答案】![]()
【解析】解:依题意知,当x1 , x2∈[1,4]时,f(x1)max≤g(x2)min , 由“对勾'函数单调性知, ![]() =2x+
=2x+ ![]() =2(x+
=2(x+ ![]() )在区间[1,4]上单调递增,
)在区间[1,4]上单调递增,
∴g(x2)min=g(1)=3;
∵ ![]() =2ax2+2x,
=2ax2+2x,
当a=0时,f(x)=2x在区间[1,4]上单调递增,∴f(x)max=f(4)=8≤3不成立,故a≠0;
∴f(x)=2ax2+2x为二次函数,其对称轴方程为:x=﹣ ![]() ,
,
当a>0时,f(x)在区间[1,4]上单调递增,f(x)max=f(4)=8≤3不成立,故a>0不成立;
当a<0时,
1°若﹣ ![]() ≤1,即a≤﹣
≤1,即a≤﹣ ![]() 时,f(x)在区间[1,4]上单调递减,
时,f(x)在区间[1,4]上单调递减,
f(x)max=f(1)=2a+2≤3恒成立,即a≤﹣ ![]() 时满足题意;
时满足题意;
2°若1<﹣ ![]() <4,即﹣
<4,即﹣ ![]() <a<﹣
<a<﹣ ![]() 时,f(x)max=f(﹣
时,f(x)max=f(﹣ ![]() )=﹣
)=﹣ ![]() ≤3,解得:﹣
≤3,解得:﹣ ![]() <a≤﹣
<a≤﹣ ![]() ;
;
3°若﹣ ![]() ≥4,即﹣
≥4,即﹣ ![]() ≤a<0时,f(x)在区间[1,4]上单调递增,
≤a<0时,f(x)在区间[1,4]上单调递增,
f(x)max=f(4)=32a+8≤3,解得a≤﹣ ![]() (﹣
(﹣ ![]() ,0),故不成立,
,0),故不成立,
综合1°2°3°知,实数a的取值范围是:(﹣∞,﹣ ![]() ].
].
所以答案是: ![]() .
.

 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了苏俄生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如表:
成绩 编号 | 1 | 2 | 3 | 4 | 5 |
物理(x) | 90 | 85 | 74 | 68 | 63 |
数学(y) | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩y对物理成绩x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() (
( ![]() 精确到0.1).若某位学生的物理成绩为80分,预测他的数学成绩;
精确到0.1).若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.(参考公式: ![]() =
= 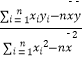 ,
, ![]() =
= ![]() ﹣
﹣ ![]() ) (参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)
) (参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)

