题目内容
20.在△ABC中,角A为钝角,AB=1,AC=3,AD为BC边上的高,已知$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围为( )| A. | ($\frac{3}{4}$,$\frac{9}{10}$) | B. | ($\frac{1}{2}$,$\frac{9}{10}$) | C. | ($\frac{3}{5}$,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
分析 $\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+k\overrightarrow{BC}$=$(1-k)\overrightarrow{AB}+k\overrightarrow{AC}$,这样即可得出x+y=1,而根据$\overrightarrow{AD}•\overrightarrow{BC}=0$便可得到$(x\overrightarrow{AB}+y\overrightarrow{AC})•(\overrightarrow{AC}-\overrightarrow{AB})=0$.进行数量积的运算便可得到3(x-y)cosA-x+9y=0,带入y=1-x可求得$x=\frac{3cosA-9}{6cosA-10}=\frac{1}{2}-\frac{2}{3cosA-5}$,由A为钝角便知-1<cosA<0,从而可求出$\frac{2}{3cosA-5}$的范围,这便可求出x的取值范围.
解答 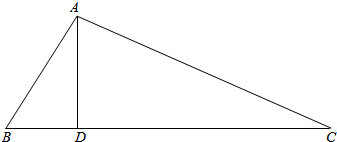 解:如图,$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}$,$\overrightarrow{BD},\overrightarrow{BC}$共线;
解:如图,$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}$,$\overrightarrow{BD},\overrightarrow{BC}$共线;
∴$\overrightarrow{BD}=k\overrightarrow{BC}=k\overrightarrow{AC}-k\overrightarrow{AB}$;
∴$\overrightarrow{AD}=(1-k)\overrightarrow{AB}+k\overrightarrow{AC}$;
又$\overrightarrow{AD}=x\overrightarrow{AB}+y\overrightarrow{AC}$;
∴x+y=1;
$\overrightarrow{AD}•\overrightarrow{BC}=0$;
∴$(x\overrightarrow{AB}+y\overrightarrow{AC})•(\overrightarrow{AC}-\overrightarrow{AB})$=3(x-y)cosA-x+9y=0;
将y=1-x带入上式并整理得:
(6cosA-10)x=3cosA-9;
∴$x=\frac{3cosA-9}{6cosA-10}=\frac{\frac{1}{2}(6cosA-10)-4}{6cosA-10}$=$\frac{1}{2}-\frac{2}{3cosA-5}$;
∵A为钝角;
∴-1<cosA<0;
∴-8<3cosA-5<-5;
∴$\frac{1}{4}<-\frac{2}{3cosA-5}<\frac{2}{5}$;
∴$\frac{3}{4}<x<\frac{9}{10}$;
∴x的取值范围为($\frac{3}{4},\frac{9}{10}$).
故选A.
点评 考查向量加法、减法的几何意义,共线向量、平面向量基本定理,以及向量垂直的充要条件,数量积的运算及其计算公式,分离常数求变量范围的方法.

 53随堂测系列答案
53随堂测系列答案| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
| A. | $\frac{2}{7π}$ | B. | $\frac{2}{5π}$ | C. | $\frac{2}{3π}$ | D. | $\frac{2}{π}$ |