题目内容
【题目】某工厂为了解用电量y与气温x℃之间的关系，随机统计了5天的用电量与当天气温，得到如下统计表：
曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
平均气温（℃） | 33 | 30 | 32 | 30 | 25 |
用电量（万度） | 38 | 35 | 41 | 36 | 30 |
xiyi=5446， xi2=4538， 
= 
， 
= 
﹣ 
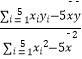（1）请根据表中的数据，求出y关于x的线性回归方程．据气象預报9月3日的平均气温是 23℃，请预测9月3日的用电量；（结果保留整数）
（2）请从表中任选两天，记用电量（万度）超过35的天数为ξ，求ξ的概率分布列，并求其数学期望和方差．
【答案】
（1）解：计算 
= 
×（33+30+32+30+25）=30，
= ×（38+35+41+36+30）=36，
又 
xiyi=5446， xi2=4538，
∴回归系数为 
= 
= 
= 
，
= ﹣ 
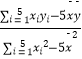=36﹣ ×30=﹣ 
，
∴回归方程为 
= x﹣ ；
当x=23时， = ×23﹣ = 
≈27.53，
即预测9月3日的用电量约为28万度；（结果保留整数）
（2）解：根据题意知，ξ的可能取值为0，1，2；
且P（ξ=0）= 
= 
，P（ξ=1）= 
= 
，P（ξ=2）= 
= 
，
所以ξ的概率分布列为
ξ | 0 | 1 | 2 |
P |
|
|
|
数学期望为E（ξ）=0× +1× +2× =1.2，
方差为D（ξ）=（0﹣1.2）2× +（1﹣1.2）2× +（2﹣1.2）2× =0.36
【解析】（1）计算 、 ，求出回归系数，写出回归方程，利用回归方程计算x=23时 的值即可；（2）根据题意知ξ的可能取值，计算对应的概率值，写出ξ的概率分布列，计算数学期望和方差．
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案，需要熟知在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．
