题目内容
【题目】设f(x)=xex(e为自然对数的底数),g(x)=(x+1)2 .
(Ⅰ)记 ![]() ,讨论函数F(x)的单调性;
,讨论函数F(x)的单调性;
(Ⅱ)令G(x)=af(x)+g(x)(a∈R),若函数G(x)有两个零点,求实数a的取值范围.
【答案】解:(Ⅰ)设F(x)= ![]() =
= ![]() ,(x≠﹣1),
,(x≠﹣1),
F′(x)= ![]() =
= 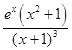 ,
,
∴当x∈(﹣∞,﹣1)时,F′(x)<0,当x∈(﹣1,+∞)时,F′(x)>0,
∴F(x)在(﹣∞,﹣1)是减函数,在(﹣1,+∞)是增函数;
(Ⅱ)G(x)=af(x)+g(x)=axex+(x+1)2,
G′(x)=a(x+1)ex+2(x+1)=(x+1)(aex+2),
当a=0时,G(x)=(x+1)2,有唯一零点:﹣1,
当a>0时,aex+2>0,则x∈(﹣∞,﹣1)时,G′(x)<0,G(x)单调递减,
当x∈(﹣1,+∞),G′(x)>0,G(x)单调递增,
G(x)极小值=G(﹣1)=﹣ ![]() <0,由G(0)=1>0,
<0,由G(0)=1>0,
∴当x∈(﹣1,+∞),G(x)有唯一的零点,
当x<﹣1时,ax<0,则ex< ![]() ,axex>
,axex> ![]() ,
,
∴G(x)> ![]() +(x+1)2=x2+(2+
+(x+1)2=x2+(2+ ![]() )x+1,
)x+1,
由△=(2+ ![]() )2﹣4×1×1=
)2﹣4×1×1= ![]() +(
+( ![]() )2>0,
)2>0,
∴t1,t2,且t1<t2,当x∈(﹣∞,t1)(t2,+∞)使得x2+(2+ ![]() )x+1>0,
)x+1>0,
取x0∈(﹣∞,﹣1)∩(﹣∞,t1),则G(x0)>0,
从而x∈(﹣∞,﹣1)时,G(x)有唯一零点,
即a>0时,函数G(x)有2个零点;
③a<0时,G′(x)=a(x+1)(ex+ ![]() ),
),
由G′(x)=0,解得:x=﹣1或ln(﹣ ![]() ),
),
若﹣1=ln(﹣ ![]() ),即a=﹣2e时,G′(x)=﹣2e(x+1)(ex﹣
),即a=﹣2e时,G′(x)=﹣2e(x+1)(ex﹣ ![]() )≤0,
)≤0,
故G(x)递减,至多有1个零点;
若﹣1>ln(﹣ ![]() ),即a<﹣2e时,G′(x)=a(x+1)(ex+
),即a<﹣2e时,G′(x)=a(x+1)(ex+ ![]() ),
),
注意到y=x+1,y=ex+ ![]() 都是增函数,
都是增函数,
故x∈(﹣∞,ln(﹣ ![]() ))时,G′(x)<0,G(x)递减,
))时,G′(x)<0,G(x)递减,
x∈(ln(﹣ ![]() ),﹣1)时,G′(x)>0,G(x)递增,
),﹣1)时,G′(x)>0,G(x)递增,
x∈(﹣1,+∞)时,G′(x)<0,G(x)递减,
又∵G(x)极小值=G(ln(﹣ ![]() ))=ln2(﹣
))=ln2(﹣ ![]() )+1>0,
)+1>0,
故G(x)至多1个零点;
若﹣1<ln(﹣ ![]() ),即﹣2e<a<0时,同理得x∈(﹣∞,﹣1)时,G′(x)<0,G(x)递减,
),即﹣2e<a<0时,同理得x∈(﹣∞,﹣1)时,G′(x)<0,G(x)递减,
x∈(﹣1,ln(﹣ ![]() ))时,G′(x)>0,G(x)递增,
))时,G′(x)>0,G(x)递增,
x∈(ln(﹣ ![]() ),+∞)时,G′(x)<0,G(x)递减,
),+∞)时,G′(x)<0,G(x)递减,
又∵G(x)极小值=G(﹣1)=﹣ ![]() >0,
>0,
∴G(x)至多1个零点,
综上,若函数G(x)有2个零点,则参数a的范围是(0,+∞)
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)求出G(x)的导数,通过讨论a的范围求出函数G(x)的极小值,结合函数的零点确定a的范围即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:
曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
用电量(万度) | 38 | 35 | 41 | 36 | 30 |
![]() xiyi=5446,
xiyi=5446, ![]() xi2=4538,
xi2=4538, ![]() =
= 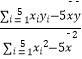 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.
【题目】某市对贫困家庭自主创业给予小额贷款补贴,每户贷款为2万元,贷款期限有6个月、12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300元、300元、400元,从2016年享受此项政策的困难户中抽取了100户进行了调查,选取贷款期限的频数如表:
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表各种贷款期限频率作为2017年贫困家庭选择各种贷款期限的概率.
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
