题目内容
【题目】数列{an}满足an=3an﹣1+3n﹣1(n∈N* , n≥2), 已知a3=95.
(1)求a1 , a2;
(2)是否存在一个实数t,使得 ![]() ,且{bn}为等差数列?若存在,则求出t的值;若不存在,请说明理由.
,且{bn}为等差数列?若存在,则求出t的值;若不存在,请说明理由.
【答案】
(1)解:n=2 时,a2=3a1+32﹣1.
n=3 时,a3=3a2+33﹣1=95,
∴a2=23
∴23=3a1+8
a1=5
(2)解:当n≥2 时
bn﹣bn﹣1= ![]() ﹣3t)
﹣3t)
= ![]()
要使{bn} 为等差数列,则必需使,∴ ![]() 即存在t=﹣
即存在t=﹣ ![]() ,使{bn} 为等差数列
,使{bn} 为等差数列
【解析】(1)将已知的递推关系中的n分别用2,3代替,列出方程组,求出a1,a2.(2)求出bn﹣bn﹣1,令1+2t=0求出t的值,保证相邻两项的差为常数,解方程求出t的值.
【考点精析】本题主要考查了等差关系的确定的相关知识点,需要掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列才能正确解答此题.
)那么这个数列就叫做等差数列才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:
曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
用电量(万度) | 38 | 35 | 41 | 36 | 30 |
![]() xiyi=5446,
xiyi=5446, ![]() xi2=4538,
xi2=4538, ![]() =
= 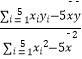 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.