Question

【题目】已知函数，

（1）当时，求的单调增区间.

（2）若对任意的实数及任意的，不等式恒成立，求实数的取值范围．

Answer 1

【答案】（1）； （2）.

【解析】

（1）将时，可得f（x）解析式，根据二次函数图象特征可得f（x）的单调增区间；

（2）结合绝对值不等式的性质，利用构造函数法进行求解即可．

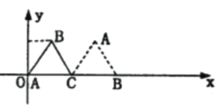
（1）当时，f（x）=x2+|x|+b=，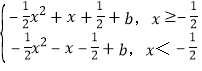

当时，对称轴x=1，开口向下；f（x）的单调增区间为；

当x时，对称轴x=﹣1，开口向下；f（x）的单调增区间为；

综上可得f（x）的单调增区间为 .

（2）因为|f（x）|≤2，所以﹣2≤ax2+|x﹣a|+b≤2，

又因为对任意的实数b∈[0，1]及任意的x∈[﹣3，3]，上式恒成立，

所以﹣2≤ax2+|x﹣a|≤1，（*），

记g（x）=ax2+|x﹣a|，

所以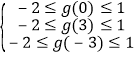，可得﹣≤a≤﹣，

又（*）式可化为﹣ax2﹣2≤|x﹣a|≤﹣ax2+1，

记h1（x）=﹣ax2+1，h2（x）=﹣ax2﹣2，k（x）=|x﹣a|，

由﹣≤a≤﹣，可知，h2（x）＜0，

所以命题转化为：只需满足以下条件

①﹣ax2﹣2=﹣x+a的较小根小于或等于﹣3，

②﹣ax2+1=x﹣a的较小根大于或等于3（或是无实根），

由①得≤﹣3，解得﹣≤a≤0；

由②得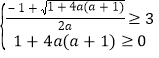或1+4a（a+1）≤0，解得a=﹣，

综上可知a的取值范围是a=﹣.