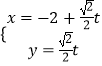题目内容
【题目】已知函数f(x)= ![]() (e为自然对数的底数).
(e为自然对数的底数).
(1)当a=b=0时,直接写出f(x)的值域(不要求写出求解过程);
(2)若a= ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(3)若f(1)=1,且方程f(x)=1在(0,1)内有解,求实数a的取值范围.
【答案】
(1)解:a=b=0时,f(x)=e﹣x,f(x)的值域是(0,+∞)
(2)解:若a= ![]() ,f(x)=(x2+bx+1)e﹣x,
,f(x)=(x2+bx+1)e﹣x,
则f′(x)=(2x+b)e﹣x﹣(x2+bx+1)e﹣x=﹣[x2+(b﹣2)x+1﹣b]e﹣x=﹣(x﹣1)[x﹣(1﹣b)]e﹣x,
由f′(x)=0得﹣(x﹣1)[x﹣(1﹣b)]=0,即x=1或x=1﹣b,
①若1﹣b=1,即b=0时,f′(x)=﹣(x﹣1)2e﹣x≤0,此时函数单调递减,单调递减区间为(﹣∞,+∞).
②若1﹣b>1,即b<0时,由f′(x)=﹣(x﹣1)[x﹣(1﹣b)]e﹣x>0得(x﹣1)[x﹣(1﹣b)]<0,即1<x<1﹣b,
此时函数单调递增,单调递增区间为(1,1﹣b),
由f′(x)=﹣(x﹣1)[x﹣(1﹣b)]e﹣x<0得(x﹣1)[x﹣(1﹣b)]>0,即x<1,或x>1﹣b,
此时函数单调递减,单调递减区间为(﹣∞,1),(1﹣b,+∞),
③若1﹣b<1,即b>0时,由f′(x)=﹣(x﹣1)[x﹣(1﹣b)]e﹣x>0得(x﹣1)[x﹣(1﹣b)]<0,即1﹣b<x<1,
此时函数单调递增,单调递增区间为(1﹣b,1),
由f′(x)=﹣(x﹣1)[x﹣(1﹣b)]e﹣x<0得(x﹣1)[x﹣(1﹣b)]>0,即x<1﹣b,或x>1,
此时函数单调递减,单调递减区间为(﹣∞,1﹣b),(1,+∞)
(3)解:若f(1)=1,则f(1)=(2a+b+1)e﹣1=1,
即2a+b+1=e,则b=e﹣1﹣2a,
若方程f(x)=1在(0,1)内有解,
即方程f(x)=(2ax2+bx+1)e﹣x=1在(0,1)内有解,
即2ax2+bx+1=ex在(0,1)内有解,
即ex﹣2ax2﹣bx﹣1=0,
设g(x)=ex﹣2ax2﹣bx﹣1,
则g(x)在(0,1)内有零点,
设x0是g(x)在(0,1)内的一个零点,
则g(0)=0,g(1)=0,知函数g(x)在(0,x0)和(x0,1)上不可能单调递增,也不可能单调递减,
设h(x)=g′(x),
则h(x)在(0,x0)和(x0,1)上存在零点,
即h(x)在(0,1)上至少有两个零点,
g′(x)=ex﹣4ax﹣b,h′(x)=ex﹣4a,
当a≤ ![]() 时,h′(x)>0,h(x)在(0,1)上递增,h(x)不可能有两个及以上零点,
时,h′(x)>0,h(x)在(0,1)上递增,h(x)不可能有两个及以上零点,
当a≥ ![]() 时,h′(x)<0,h(x)在(0,1)上递减,h(x)不可能有两个及以上零点,
时,h′(x)<0,h(x)在(0,1)上递减,h(x)不可能有两个及以上零点,
当 ![]() <a<
<a< ![]() 时,令h′(x)=0,得x=ln(4a)∈(0,1),
时,令h′(x)=0,得x=ln(4a)∈(0,1),
则h(x)在(0,ln(4a))上递减,在(ln(4a),1)上递增,h(x)在(0,1)上存在最小值h(ln(4a)).
若h(x)有两个零点,则有h(ln(4a))<0,h(0)>0,h(1)>0,
h(ln(4a))=4a﹣4aln(4a)﹣b=6a﹣4aln(4a)+1﹣e, ![]() <a<
<a< ![]() ,
,
设φ(x)= ![]() x﹣xlnx+1﹣x,(1<x<e),
x﹣xlnx+1﹣x,(1<x<e),
则φ′(x)= ![]() ﹣lnx,
﹣lnx,
令φ′(x)= ![]() ﹣lnx=0,得x=
﹣lnx=0,得x= ![]() ,
,
当1<x< ![]() 时,φ′(x)>0,此时函数φ(x)递增,
时,φ′(x)>0,此时函数φ(x)递增,
当 ![]() <x<e时,φ′(x)<0,此时函数φ(x)递减,
<x<e时,φ′(x)<0,此时函数φ(x)递减,
则φ(x)max=φ( ![]() )=
)= ![]() +1﹣e<0,
+1﹣e<0,
则h(ln(4a))<0恒成立,
由h(0)=1﹣b=2a﹣e+2>0,h(1)=e﹣4a﹣b>0,
得 ![]() <a<
<a< ![]() ,
,
当 ![]() <a<
<a< ![]() 时,设h(x)的两个零点为x1,x2,则g(x)在(0,x1)递增,
时,设h(x)的两个零点为x1,x2,则g(x)在(0,x1)递增,
在(x1,x2)上递减,在(x2,1)递增,
则g(x1)>g(0)=0,
g(x2)<g(1)=0,
则g(x)在(x1,x2)内有零点,
综上,实数a的取值范围是( ![]() ,
, ![]() )
)
【解析】(1)求出f(x)的导数,根据指数函数的性质求出函数的值域即可;(2)由a的值,求函数的导数,利用函数单调性和导数之间的关系即可求函数f(x)的单调区间;(3)根据函数与方程之间的关系转化为函数存在零点问题,构造函数,求函数的导数,利用函数极值和函数零点之间的关系进行转化求解即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.