Question

【题目】某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队．经过本地养鱼场年利润率的调研，得到如图所示年利润率的频率分布直方图．对远洋捕捞队的调研结果是：年利润率为60%的可能性为0.6，不赔不赚的可能性为0.2，亏损30%的可能性为0.2．假设该公司投资本地养鱼场的资金为x（x≥0）千万元，投资远洋捕捞队的资金为y（y≥0）千万元．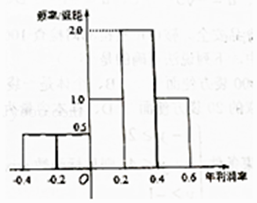
（1）利用调研数据估计明年远洋捕捞队的利润ξ的分布列和数学期望Eξ．
（2）为确保本地的鲜鱼供应，市政府要求该公司对本地养鱼场的投资不得低于远洋捕捞队的一半．适用调研数据，给出公司分配投资金额的建议，使得明年两个项目的利润之和最大．

Answer 1

【答案】
（1）解：随机变量ξ的可能取值为0.6y，0，﹣0.3y，

随机变量ξ的分布列为，

ξ	0.6y	0	﹣0.3y
P	0.6	0.2	0.2

∴Eξ=0.36y﹣0.06y=0.3y

（2）解：根据题意得，x，y满足的条件为 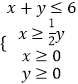①，

由频率分布直方图得本地养鱼场的年平均利润率为：

﹣0.3×0.2×0.5+（﹣0.1）×0.2×0.5+0.1×0.2×1.0+0.3×0.2×2.0+0.5×0.2×1.0=0.20，

∴本地养鱼场的年利润为0.20x千万元，

∴明年连个个项目的利润之和为z=0.2x+0.3y，

作出不等式组①所表示的平面区域若下图所示，即可行域．

当直线z=0.2x+0.3y经过可行域上的点M时，截距 最大，即z最大．

解方程组 ，得

∴z的最大值为：0.20×2+0.30×4=1.6千万元．

即公司投资本地养鱼场和远洋捕捞队的资金应分别为2千万元、4千万元时，明年两个项目的利润之和的最大值为1.6千万元．

【解析】（1）随机变量ξ的可能取值为0.6y，0，﹣0.3y，分别求出相应的概率，由此能求出随机变量ξ的分布列和Eξ．（2）根据题意得，x，y满足的条件，由频率分布直方图求出本地养鱼场的年平均利润率为0.20x千万元，从而明年连个个项目的利润之和为z=0.2x+0.3y，作出x，y满足的可行域，由此能求出公司投资本地养鱼场和远洋捕捞队的资金应分别为2千万元、4千万元时，明年两个项目的利润之和的最大值为1.6千万元．
【考点精析】掌握频率分布直方图是解答本题的根本，需要知道频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息．