题目内容
.已知正四面体的高为H,它的内切球半径为R,则R︰H=______________.
1:4
略
解:设正四面体的内切圆园心为O,连接O到正四面体的各个顶点,把正四面体分割成四个小的四面体
则内切圆到各个面的距离就是内切圆的半径R,正四面体的体积可以表示为:
S正四面体=4*(1/3*S底面积*R)
又有S正四面体=1/3*S底面积*H
所以:4*(1/3*S底面积*R=1/3*S底面积*H
得:R︰H=1:4
故答案为1:4
解:设正四面体的内切圆园心为O,连接O到正四面体的各个顶点,把正四面体分割成四个小的四面体
则内切圆到各个面的距离就是内切圆的半径R,正四面体的体积可以表示为:
S正四面体=4*(1/3*S底面积*R)
又有S正四面体=1/3*S底面积*H
所以:4*(1/3*S底面积*R=1/3*S底面积*H
得:R︰H=1:4
故答案为1:4

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
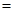 1,AD
1,AD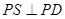 .
.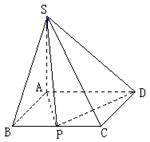
 和矩形
和矩形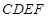 所在的平面互相垂直,
所在的平面互相垂直,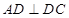 ,
,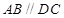 ,
,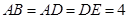 ,
,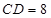 .
. 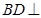 平面
平面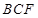 ;
;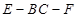 的平面角为
的平面角为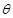 ,求
,求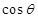 的值;
的值;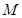 为
为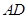 的中点,在
的中点,在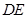 上是否存在一点
上是否存在一点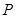 ,使得
,使得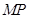 ∥平面
∥平面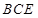 ?若存在,求出
?若存在,求出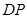 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
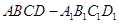 中,
中, 与平面
与平面 所成角的余弦值为( ▲ )
所成角的余弦值为( ▲ )
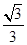

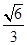
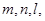 两个不重合的平面
两个不重合的平面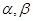 ,给出下列四个命题:
,给出下列四个命题: 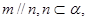 则
则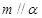 ;
;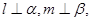 且
且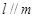 则
则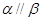 ;
;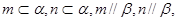 则
则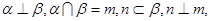 则
则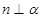 . 其中真命题是 ( )
. 其中真命题是 ( )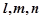 是三条不同的直线,
是三条不同的直线,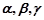 是三个不同的平面,则下列命题中为假命题的是
是三个不同的平面,则下列命题中为假命题的是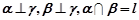 ,则
,则
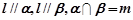 ,则
,则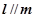
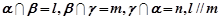 ,则
,则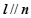
 ,则
,则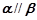 或
或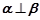
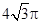 的球的内接正方体的棱长为_____________。
的球的内接正方体的棱长为_____________。 B
B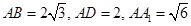 ,则点
,则点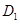 到直线AC的距离是
到直线AC的距离是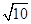
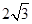
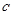 ,G、H分别是BE、ED的中点,则GH到平面ABD的距离是______
,G、H分别是BE、ED的中点,则GH到平面ABD的距离是______