题目内容
【题目】选修4-4：坐标系与参数方程
在直角坐标系中，已知曲线
的参数方程为
（
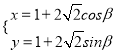为参数），在极坐标系中，直线
的方程为： 
，直线
的方程为
．
（Ⅰ）写出曲线
的直角坐标方程，并指出它是何种曲线；
（Ⅱ）设
与曲线
交于
两点， 
与曲线
交于
两点，求四边形
面积的取值范围．
【答案】(1) 以
为圆心， 
为半径的圆；（2）
.
【解析】试题分析：（Ⅰ）利用平方法可消去参数，从而可得曲线
的直角坐标方程，进而得它是何种曲线；（Ⅱ）设
， 
，曲线
的方程化成极坐标方程，将曲线
的方程化成极坐标方程得： 
，∴
， 
，从而可得结果.
试题解析：（Ⅰ）由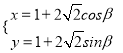
（
为参数）消去参数
得： 
，
∴曲线
是以
为圆心， 
为半径的圆．
（Ⅱ）设
， 
，
∵
三点共线，则
①，
将曲线
的方程化成极坐标方程得： 
，∴
，代入①得： 
，
用
代
得： 
又∵
，∴
，
∴
，
∵
，∴
练习册系列答案
相关题目
