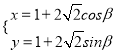题目内容
【题目】用数学归纳法证明:12﹣22+32﹣42+…+(﹣1)n﹣1n2=(﹣1)n﹣1 ![]() .
.
【答案】证明:①当n=1时,左边=1,右边=(﹣1)0![]() =1, 故:左边=右边,
=1, 故:左边=右边,
∴当n=1时,等式成立;
②假设n=k时,等式成立,即 12﹣22+32﹣42+…+(﹣1)k﹣1k2=(﹣1)k﹣1 ![]() .
.
那么12﹣22+32﹣42+…+(﹣1)k﹣1k2+(﹣1)k(k+1)2
=(﹣1)k﹣1 ![]() +(﹣1)k(k+1)2
+(﹣1)k(k+1)2
=(﹣1)k![]() (﹣k+2k+2)
(﹣k+2k+2)
=(﹣1)(k+1)﹣1![]()
即当n=k+1时,等式也成立.
根据①和②可知等式对任何n∈N+都成立
【解析】用数学归纳法证明问题的步骤是:第一步,验证当n=n0时命题成立,第二步假设当n=k时命题成立,那么再证明当n=k+1时命题也成立.关键是第二步中要充分用上归纳假设的结论.
【考点精析】根据题目的已知条件,利用数学归纳法的定义的相关知识可以得到问题的答案,需要掌握数学归纳法是证明关于正整数n的命题的一种方法.

练习册系列答案
相关题目