题目内容
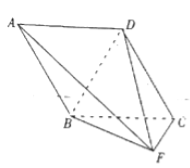
【题目】如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四点F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求证:平面CBE⊥平面EDB;
(Ⅲ)当x=2时,求二面角F﹣EB﹣C的大小.
【答案】证明:(Ⅰ)∵AF∥DE,AB∥CD,AF∩AB=A,DE∩DC=D,
∴平面ABF∥平面DCE,
∵平面ADEF⊥平面ABCD,
∴FB∥CE,∴△ABF~△DCE,
∵AB=a,∴ED=a,CD=2a,AF= ![]() ,由相似比得
,由相似比得 ![]() ,即
,即 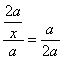 ,得x=4
,得x=4
(Ⅱ)连接BD,设AB=1,则AB=AD=1,CD=2,可得BD= ![]() ,取CD的中点M,则MD与AB平行且相等,
,取CD的中点M,则MD与AB平行且相等,
则△BMD为等腰直角三角形,则BC=BD= ![]() ,
,
∵BD2+BC2=CD2 ,
∴BC⊥BD.
∵平面四边形ADEF与梯形ABCD所在的平面互相垂直,平面ADEF∩平面ABCD=AD,ED⊥AD,
∴ED⊥平面ABCD,BC⊥DE,
又∵ED∩BD=D,
∴BC⊥平面BDE.
又∵BC平面BCE,
∴平面BDE⊥平面BEC.
( III)建立空间坐标系如图:设AB=1,
∵x=2,∴CD=2,
则F(1,0,1),B(1,1,0),E(0,0,1),C(0,2,0),![]() =(1,0,0),
=(1,0,0), ![]() =(1,1,﹣1),
=(1,1,﹣1), ![]() =(0,2,﹣1),
=(0,2,﹣1),
设平面EF的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则由 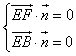 得
得 ![]() ,则取
,则取 ![]() =(0,1,1),
=(0,1,1),
设平面EBC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 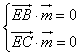 ,得
,得 ![]() ,令y=1,则z=2,x=1,即
,令y=1,则z=2,x=1,即 ![]() =(1,1,2),
=(1,1,2),
则cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
则< ![]() ,
, ![]() >=30°,
>=30°,
∵二面角F﹣EB﹣C是钝二面角,
∴二面角F﹣EB﹣C的大小为150°.
【解析】(Ⅰ)根据四点F、B、C、E共面,以及三角形相似建立方程关系进行求解;(Ⅱ) 根据面面垂直的判定定理即可证明平面BDE⊥平面BEC;(Ⅲ)建立空间坐标系,求出平面的法向量,利用向量法即可.
【考点精析】利用直线与平面垂直的判定对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案