Question

【题目】[选修4―4：坐标系与参数方程]

在直角坐标系xOy中，直线l1的参数方程为（t为参数），直线l2的参数方程为.设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．

（1）写出C的普通方程；

（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ(cosθ+sinθ) =0，M为l3与C的交点，求M的极径.

Answer 1

【答案】（1）；（2）.

【解析】（1）利用加减消元法将直线， 的参数方程化为普通方程，再消去得C的普通方程，注意；（2）联立两个极坐标方程可得，代入极坐标方程进行计算可得极径为.

试题解析：（1）消去参数得的普通方程；消去参数m得l2的普通方程.

设,由题设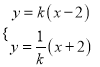得，消去k得.

所以C的普通方程为.

（2）C的极坐标方程为.

联立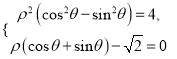得.

故，从而.

代入得，所以交点M的极径为.