题目内容
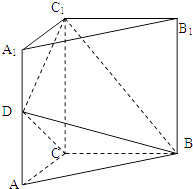
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据题设条件可以得出AB⊥AP,CD⊥PD.而AB//CD,就可证明出AB⊥平面PAD.
进而证明出平面PAB⊥平面PAD.(2)先找出AD中点,找出相互垂直的线,建立以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴正方向,
轴正方向, ![]() 为单位长的空间直角坐标系,列出所需要的点的坐标,设
为单位长的空间直角坐标系,列出所需要的点的坐标,设![]() 是平面
是平面![]() 的法向量,
的法向量, ![]() 是平面
是平面![]() 的法向量,根据垂直关系,求出
的法向量,根据垂直关系,求出![]() 和
和![]() ,利用数量积公式可求出二面角的平面角.
,利用数量积公式可求出二面角的平面角.
试题解析:(1)由已知![]() ,得AB⊥AP,CD⊥PD.
,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,从而AB⊥平面PAD.
又AB ![]() 平面PAB,所以平面PAB⊥平面PAD.
平面PAB,所以平面PAB⊥平面PAD.
(2)在平面![]() 内做
内做![]() ,垂足为
,垂足为![]() ,
,
由(1)可知, ![]() 平面
平面![]() ,故
,故![]() ,可得
,可得![]() 平面
平面![]() .
.
以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴正方向,
轴正方向, ![]() 为单位长,建立如图所示的空间直角坐标系
为单位长,建立如图所示的空间直角坐标系![]() .
.
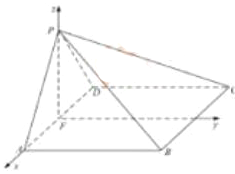
由(1)及已知可得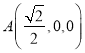 ,
, 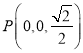 ,
, 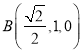 ,
,  .
.
所以 ,
, ![]() ,
,  ,
, ![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
![]() ,即
,即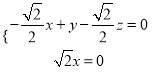 ,
,
可取![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
![]() ,即
,即 ,
,
可取![]() .
.
则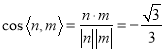 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
点睛:高考对空间向量与立体几何的考查主要体现在以下几个方面:①求异面直线所成的角,关键是转化为两直线的方向向量的夹角;②求直线与平面所成的角,关键是转化为直线的方向向量和平面的法向量的夹角;③求二面角,关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目