题目内容
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,F为椭圆的右焦点,M、N两点在椭圆C上,且
,F为椭圆的右焦点,M、N两点在椭圆C上,且 =λ
=λ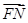 (λ>0),定点A(-4,0).
(λ>0),定点A(-4,0).
(1)求证:当λ=1时, ⊥
⊥ ;
;
(2)若当λ=1时,有 ·
· =
= ,求椭圆C的方程..
,求椭圆C的方程..
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,F为椭圆的右焦点,M、N两点在椭圆C上,且
,F为椭圆的右焦点,M、N两点在椭圆C上,且 =λ
=λ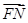 (λ>0),定点A(-4,0).
(λ>0),定点A(-4,0).(1)求证:当λ=1时,
 ⊥
⊥ ;
;(2)若当λ=1时,有
 ·
· =
= ,求椭圆C的方程..
,求椭圆C的方程..(1)见解析(2)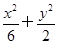 =1
=1
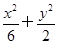 =1
=1(1)证明:设M(x1,y1),N(x2,y2),F(c,0),则 =(c-x1,-y1),
=(c-x1,-y1),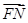 =(x2-c,y2).当λ=1时,
=(x2-c,y2).当λ=1时, =
=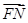 ,∴-y1=y2,x1+x2=2c.∵M、N两点在椭圆C上,∴
,∴-y1=y2,x1+x2=2c.∵M、N两点在椭圆C上,∴ =a2
=a2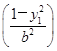 ,
,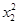 =a2
=a2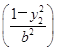 ,∴
,∴ =
=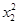 .若x1=-x2,则x1+x2=0≠2c(舍去),∴x1=x2,∴
.若x1=-x2,则x1+x2=0≠2c(舍去),∴x1=x2,∴ =(0,2y2),
=(0,2y2), =(c+4,0),∴
=(c+4,0),∴ ·
· =0,∴
=0,∴ ⊥
⊥ .
.
(2)解:当λ=1时,由(1)知x1=x2=c,
∴M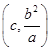 ,N
,N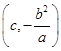 ,∴
,∴ =
= ,
, =
=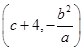 ,
,
∴ ·
· =(c+4)2-
=(c+4)2-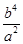 =
= .(*)
.(*)
∵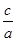 =
= ,∴a2=
,∴a2= c2,b2=
c2,b2=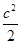 ,代入(*)式得
,代入(*)式得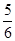 c2+8c+16=
c2+8c+16= ,∴c=2或c=-
,∴c=2或c=-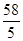 (舍去).∴a2=6,b2=2,∴椭圆C的方程为
(舍去).∴a2=6,b2=2,∴椭圆C的方程为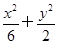 =1
=1
 =(c-x1,-y1),
=(c-x1,-y1),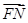 =(x2-c,y2).当λ=1时,
=(x2-c,y2).当λ=1时, =
=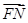 ,∴-y1=y2,x1+x2=2c.∵M、N两点在椭圆C上,∴
,∴-y1=y2,x1+x2=2c.∵M、N两点在椭圆C上,∴ =a2
=a2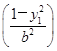 ,
,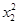 =a2
=a2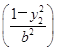 ,∴
,∴ =
=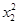 .若x1=-x2,则x1+x2=0≠2c(舍去),∴x1=x2,∴
.若x1=-x2,则x1+x2=0≠2c(舍去),∴x1=x2,∴ =(0,2y2),
=(0,2y2), =(c+4,0),∴
=(c+4,0),∴ ·
· =0,∴
=0,∴ ⊥
⊥ .
.(2)解:当λ=1时,由(1)知x1=x2=c,
∴M
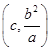 ,N
,N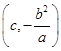 ,∴
,∴ =
= ,
, =
=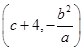 ,
,∴
 ·
· =(c+4)2-
=(c+4)2-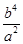 =
= .(*)
.(*)∵
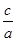 =
= ,∴a2=
,∴a2= c2,b2=
c2,b2=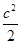 ,代入(*)式得
,代入(*)式得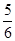 c2+8c+16=
c2+8c+16= ,∴c=2或c=-
,∴c=2或c=-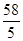 (舍去).∴a2=6,b2=2,∴椭圆C的方程为
(舍去).∴a2=6,b2=2,∴椭圆C的方程为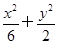 =1
=1
练习册系列答案
相关题目
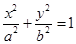 (
(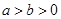 )的短轴长为2,离心率为
)的短轴长为2,离心率为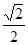 .
.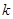 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足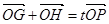 (O为坐标原点),当
(O为坐标原点),当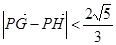 时,求实数
时,求实数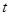 的取值范围?
的取值范围?
 与双曲线
与双曲线 在交点处正交,则椭圆
在交点处正交,则椭圆

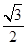

 =1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为
=1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为 ,点M的横坐标为
,点M的横坐标为 .
.
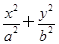 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.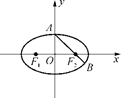
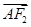 =2
=2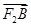 ,
,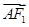 ·
·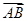 =
=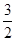 ,求椭圆的方程.
,求椭圆的方程. =1(a>b>0)的左、右焦点,若在直线x=
=1(a>b>0)的左、右焦点,若在直线x= 上存在点P,使线段PF1的中垂线过点F2,则椭圆的离心率的取值范围是________.
上存在点P,使线段PF1的中垂线过点F2,则椭圆的离心率的取值范围是________. 的椭圆
的椭圆 与双曲线
与双曲线 有相同的焦点,且椭圆长轴的端点,短轴的端点,焦点到双曲线的一条渐近线的距离依次构成等差数列,则双曲线
有相同的焦点,且椭圆长轴的端点,短轴的端点,焦点到双曲线的一条渐近线的距离依次构成等差数列,则双曲线 B.
B. C.
C. D.
D.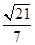
 的最小值是 .
的最小值是 .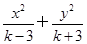 =1表示椭圆,则k的取值范围是________.
=1表示椭圆,则k的取值范围是________.