题目内容
已知点F1、F2分别是椭圆x2+2y2=2的左、右焦点,点P是该椭圆上的一个动点,则
的最小值是 .
的最小值是 .2
设P(x,y),则x2+2y2=2,
由椭圆方程
+y2=1可知,a=
,b=1,c=1,
∴F1(-1,0),F2(1,0).
∴
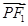=(-1-x,-y),
=(1-x,-y),
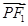∴+=(-2x,-2y).
∴|+|=
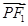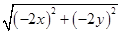
=2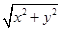
=2
=2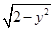
.
∵y2≤1,
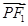∴|+|的最小值是2.
由椭圆方程
+y2=1可知,a=,b=1,c=1,∴F1(-1,0),F2(1,0).
∴
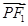=(-1-x,-y),=(1-x,-y),∴
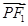+=(-2x,-2y).∴|
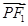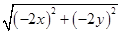
+|= =2
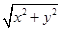
=2
=2
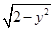.∵y2≤1,
∴|
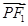+|的最小值是2.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
＝1(a＞b＞0)的离心率为
，F为椭圆的右焦点，M、N两点在椭圆C上，且
＝λ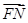
(λ＞0)，定点A(－4，0)．
⊥
；
·
＝
，求椭圆C的方程．.
+
=1(a>b>0)的焦距为4,且过点P(
,
).
：方程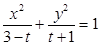
所表示的曲线为焦点在
轴上的椭圆；命题
：实数
满足不等式
.
的取值范围．
+
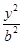=1(a>b>0)与双曲线C2:x2-
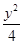=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
+
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
+
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
,则C的离心率为( )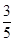
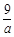(其中a是正常数)，则点P的轨迹是（ ）
分别为椭圆
的左、右焦点,点
在椭圆上,若
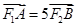,则点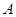
的坐标是__________