题目内容
【题目】如图,四棱锥P-ABCD的底面为矩形,且AB=![]() ,BC=1,E,F分别为AB,PC中点.
,BC=1,E,F分别为AB,PC中点.

(1)求证:EF∥平面PAD;
(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.
【答案】证明:(1)方法一:取线段PD的中点M,连结FM,AM.
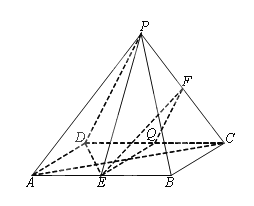
因为F为PC的中点,所以FM∥CD,且FM=![]() CD.
CD.
因为四边形ABCD为矩形,E为AB的中点,
所以EA∥CD,且EA=![]() CD.
CD.
所以FM∥EA,且FM=EA.
所以四边形AEFM为平行四边形.
所以EF∥AM. ……………………… 5分
又AM平面PAD,EF平面PAD,所以EF∥平面PAD. ………7分
方法二:连结CE并延长交DA的延长线于N,连结PN.
因为四边形ABCD为矩形,所以AD∥BC,
所以∠BCE=∠ANE,∠CBE=∠NAE.
又AE=EB,所以△CEB≌△NEA.所以CE=NE.
又F为PC的中点,所以EF∥NP.………… 5分
又NP平面PAD,EF平面PAD,所以EF∥平面PAD. ……………7分
方法三:取CD的中点Q,连结FQ,EQ.
在矩形ABCD中,E为AB的中点,所以AE=DQ,且AE∥DQ.
所以四边形AEQD为平行四边形,所以EQ∥AD.
又AD平面PAD,EQ平面PAD,所以EQ∥平面PAD. ………………2分
因为Q,F分别为CD,CP的中点,所以FQ∥PD.
又PD平面PAD,FQ平面PAD,所以FQ∥平面PAD.
又FQ,EQ平面EQF,FQ∩EQ=Q,所以平面EQF∥平面PAD.…………… 5分
因为EF平面EQF,所以EF∥平面PAD. ……………………………… 7分
(2)设AC,DE相交于G.
在矩形ABCD中,因为AB=![]() BC,E为AB的中点.所以
BC,E为AB的中点.所以![]() =
=![]() =
=![]() .
.
又∠DAE=∠CDA,所以△DAE∽△CDA,所以∠ADE=∠DCA.
又∠ADE+∠CDE=∠ADC=90°,所以∠DCA+∠CDE=90°.
由△DGC的内角和为180°,得∠DGC=90°.即DE⊥AC. ……………………… 10分
因为平面PAC⊥平面ABCD 因为DE平面ABCD,所以DE⊥平面PAC,
又DE平面PDE,所以平面PAC⊥平面PDE. ………………………… 14分
【解析】略

【题目】某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(1)完成下列![]() 列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族" | 属于“观望者" | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求![]() 的分布列及数学期望.
的分布列及数学期望.
附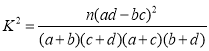 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | p>0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |