题目内容
【题目】设函数![]() .若
.若![]() 在
在![]() 上的最大值为2,则实数a所有可能的取值组成的集合是________.
上的最大值为2,则实数a所有可能的取值组成的集合是________.
【答案】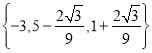
【解析】
根据函数的最大值,依据![]() 可求出
可求出![]() 的两种情况.讨论
的两种情况.讨论![]() 的不同取值,去掉内层的绝对值,利用导数分析三次函数的极值点,进而求得最大值与最小值.通过函数的上下平移,结合最值即可求得
的不同取值,去掉内层的绝对值,利用导数分析三次函数的极值点,进而求得最大值与最小值.通过函数的上下平移,结合最值即可求得![]() 的所有取值.
的所有取值.
因为函数![]() .若
.若![]() 在
在![]() 上的最大值为2
上的最大值为2
所以![]() ,即
,即![]()
当![]() 时,不等式化为
时,不等式化为![]() ,解得
,解得![]()
当![]() 时,不等式化为
时,不等式化为![]() ,解得
,解得![]()
由以上可知:
(1) 当![]() 时,函数解析式可化为
时,函数解析式可化为![]()
令![]() ,则
,则![]()
当![]() 时解得
时解得![]()
当![]() 时,
时, ![]() ,即
,即![]() 在
在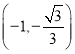 上单调递增
上单调递增
当![]() 时,
时, ![]() ,即
,即![]() 在
在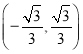 上单调递减
上单调递减
当![]() 时,
时, ![]() ,即
,即![]() 在
在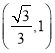 上单调递增.
上单调递增.
所以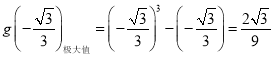 ,
,
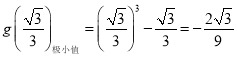
![]()
当![]() 时,
时, ![]() 向下平移
向下平移![]() 个单位可得
个单位可得![]() 的图像
的图像
因为![]() 在
在![]() 上的最大值为2
上的最大值为2
所以只需满足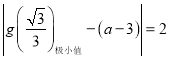 即可,即
即可,即![]() ,解得
,解得![]() ,或
,或![]() (舍)
(舍)
当![]() 时,
时, ![]() 向上平移
向上平移![]() 个单位可得到
个单位可得到![]() 的图像
的图像
由![]() 在
在![]() 上的最大值为2
上的最大值为2
可知只需满足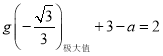 即可.即
即可.即![]() ,解得
,解得![]() ,符合题意
,符合题意
(2) 当![]() ,函数解析式可化为
,函数解析式可化为![]()
令![]() ,则
,则![]()
所以![]() 在
在![]() 上单调递增
上单调递增
则![]()
![]()
当![]() 时,
时,![]() 向下平移
向下平移![]() 个单位可得
个单位可得![]()
由![]() 在
在![]() 上的最大值为2
上的最大值为2
只需![]() ,即
,即![]() 解得
解得![]() 或
或![]() (舍)
(舍)
当![]() 时,
时, ![]() 向上平移
向上平移![]() 个单位可得
个单位可得![]()
由![]() 在
在![]() 上的最大值为2
上的最大值为2
只需![]() ,即
,即![]() 解得
解得![]() 或
或![]() (舍)
(舍)
综上可知,满足条件的所有可能的![]() 为
为![]()
![]() 和
和![]()
故答案为: 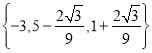

【题目】根据幼儿身心发展的特征,幼儿园通常着重在健康、科学、社会、语言、艺术五大领域对幼儿展开全方位的教育和培养.经调查发现,一个幼儿除了在幼儿园进行五大领域的系统学习之外,还会报一些课外兴趣班.而家长朋友们对于是否额外报这些课外兴趣班的态度也是不一样的.某调查机构对某幼儿园的100名幼儿家长就孩子是否报课外兴趣班的赞同程度进行调查统计,得到家长对幼儿报课外兴趣班赞同度![]() 的频数分布表:
的频数分布表:
赞同度 |
|
|
|
|
|
家长数 | 2 | 12 | 14 | 28 | 44 |
(1)分别计算对幼儿报兴趣班的赞同度不低于![]() 的家长比例和对幼儿报兴趣班的赞同度低于
的家长比例和对幼儿报兴趣班的赞同度低于![]() 的家长比例;
的家长比例;
(2)求家长对幼儿报兴趣班的赞同度的平均数与方差的估计值.(同一组中的数据用该组区间的中点值代替)