题目内容
【题目】已知函数![]() .
.
(1)讨论f(x)的单调性;
(2)证明:当﹣1<a<0时,f(x)存在唯一的零点x0,且x0随着a的增大而增大.
【答案】(1)答案不唯一,具体见解析(2)证明见解析
【解析】
(1)先求得函数![]() 的定义域,求得函数的导函数
的定义域,求得函数的导函数![]() ,对
,对![]() 分成
分成![]() 等四种情况进行分类讨论,由此求得
等四种情况进行分类讨论,由此求得![]() 的单调区间.
的单调区间.
(2)![]() 时,由(1)得到
时,由(1)得到![]() 的单调性,结合零点存在性定理判断出
的单调性,结合零点存在性定理判断出![]() 存在唯一零点
存在唯一零点![]() .令
.令![]() ,由此对
,由此对![]() 分离常数,利用导数证得
分离常数,利用导数证得![]() 随
随![]() 增大而增大.
增大而增大.
(1)f(x)的定义域为(0,+∞);
![]() ;
;
①当a=0时,![]() ,则f(x)在(0,+∞)上单调递减;
,则f(x)在(0,+∞)上单调递减;
②当a>0时,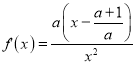 ,而
,而![]() ;
;
则f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
③当﹣1≤a<0时,f′(x)<0,则f(x)在(0,+∞)上单调递减;
④当a<﹣1时,f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
综上,当a<﹣1时,f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当﹣1≤a≤0时,f′(x)<0,则f(x)在(0,+∞)上单调递减;
当a>0时,f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(2)由(1)得当﹣1<a<0时,f(x)在(0,+∞)上单调递减;
∴f(x)至多有一个零点;
又﹣1<a<0;
∴![]() ,f(1)=a+1>0,
,f(1)=a+1>0,![]() ;
;
令g(x)=x﹣1﹣lnx,则![]() ;
;
∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
g(x)≥g(1)=0,即x﹣1﹣lnx≥0,当且仅当x=1时取等号;
∴![]() ;
;
∴f(x)存在唯一得零点![]() ;
;
由f(x0)=0,得![]() ,即
,即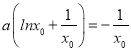 ;
;
∵x0∈(1,+∞),![]() ;
;
∴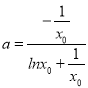 ,即a是x0的函数;
,即a是x0的函数;
设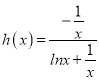 ,x∈(1,+∞),则
,x∈(1,+∞),则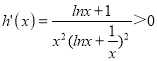 ;
;
∴h(x)为(1,+∞)上的增函数;
∴![]() 随
随![]() 增大而增大,反之亦成立.
增大而增大,反之亦成立.
∴x0随着a的增大而增大.

练习册系列答案
相关题目