题目内容
5.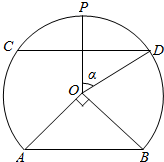 如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.
如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.(1)求y关于α的函数的解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
分析 (1)根据已知,将弧AC和弦CD的长度相加,可得y关于α的函数的解析式,结合∠AOB=$\frac{π}{2}$,求出∠POD的范围,可得该函数的定义域;
(2)利用导数法,分析函数的单调性,进而可得函数的最大值.
解答 解:(1)由题意得,
y=$\sqrt{2}$•($\frac{3π}{4}$-α)+$\sqrt{2}$•sinα×2=$\frac{3\sqrt{2}}{4}π$-$\sqrt{2}$α+2$\sqrt{2}$sinα,
∵∠AOB=$\frac{π}{2}$,∠POD=α,
∴0<2α<2π-$\frac{π}{2}$,
∴0<α<$\frac{3π}{4}$;
函数的定义域为{α|0<α<$\frac{3π}{4}$};
(2)y′=$\sqrt{2}$-2$\sqrt{2}$cosα,
令y′=0解得,α=$\frac{π}{3}$,
故当α=$\frac{π}{3}$时,观光路线总长最大,
最大值为$\frac{5\sqrt{2}}{12}π$+$\sqrt{6}$(km).
点评 本题考查了学生将实际问题转化为数学问题的能力,属于中档题.

练习册系列答案
相关题目
14.由一排编号为1至7的七个座位连成一排,现有2名语文老师和2名数学老师共4人就坐,要求同一学科的老师不能相邻,有多少种不同的坐法( )
| A. | 400 | B. | 330 | C. | 440 | D. | 324 |