题目内容
15.求证:在二次函数f(x)=ax2+bx+c中,若x1≠x2,则使“f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$成立”的充要条件是“a>0”分析 利用作差法,结合充分条件和必要条件的定义进行证明即可.
解答 证明:$\frac{f({x}_{1})+f({x}_{2})}{2}$-f($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{1}{2}$(ax12+bx1+c+ax22+bx2+c)-a($\frac{{x}_{1}+{x}_{2}}{2}$)2-b•($\frac{{x}_{1}+{x}_{2}}{2}$)-c
=$\frac{1}{2}$(ax12+bx1+ax22+bx2)-a($\frac{{x}_{1}+{x}_{2}}{2}$)2-b•($\frac{{x}_{1}+{x}_{2}}{2}$)
=$\frac{1}{2}$(ax12+ax22)-a($\frac{{x}_{1}+{x}_{2}}{2}$)2
=$\frac{1}{4}$(2ax12+2ax22-ax12-ax22-2ax1x2)
=$\frac{1}{4}$(ax12+ax22-2ax1x2)
=$\frac{1}{4}$a(x1-x2)2,
∵x1≠x2,∴(x1-x2)2>0,
若f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$成立,则$\frac{f({x}_{1})+f({x}_{2})}{2}$-f($\frac{{x}_{1}+{x}_{2}}{2}$)>0,此时a>0,
反之,若a>0,则$\frac{f({x}_{1})+f({x}_{2})}{2}$-f($\frac{{x}_{1}+{x}_{2}}{2}$)>0,即f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$成立,
故使“f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$成立”的充要条件是“a>0”.
点评 本题主要考查充分条件和必要条件的证明,利用作差法,结合函数的性质是解决本题的关键.

| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ |
| A. | $\frac{1}{21}$ | B. | -$\frac{1}{21}$ | C. | $\frac{1}{20}$ | D. | -$\frac{1}{20}$ |
| A. | -1<m<4 | B. | -1<m<3 | C. | 1<m<4 | D. | 1<m<3 |
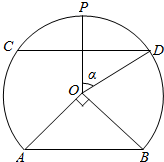 如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.
如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.