题目内容
10.命题“?x∈(-1,2),ax+2≠0”为假命题的一个充分不必要条件是a∈(2,+∞).分析 先求出命题“?x∈(-1,2),ax+2≠0”为假命题的充要条件,进而可得答案.
解答 解:若命题“?x∈(-1,2),ax+2≠0”为假命题,
则命题“?x∈(-1,2),ax+2=0”为真命题,
即ax+2=0的根x=-$\frac{2}{a}$∈(-1,2),
解得:a∈(-∞,-1)∪(2,+∞),
即命题“?x∈(-1,2),ax+2≠0”为假命题的充要条件为a∈(-∞,-1)∪(2,+∞),
由(2,+∞)?(-∞,-1)∪(2,+∞),
故a∈(2,+∞)就为命题“?x∈(-1,2),ax+2≠0”为假命题的一个充分不必要条件,
故答案为:a∈(2,+∞)(答案不唯一)
点评 本题考查充分必要条件的概念,属于基础题.

练习册系列答案
相关题目
19.设[x]表示不超过实数x的最大整数,如[2.6]=2,[-2.6]=-3,设g(x)=$\frac{{a}^{x}}{{a}^{x}+1}$(a>0且a≠1),那么函数f(x)=[g(x)-$\frac{1}{2}$]+[g(-x)-$\frac{1}{2}$]的值域为( )
| A. | {-1,0,1} | B. | {0,1} | C. | {1,-1} | D. | {-1,0} |
20.若数列{an}的通项公式是an=(-1)n•$\frac{1}{2n+1}$,则a10=( )
| A. | $\frac{1}{21}$ | B. | -$\frac{1}{21}$ | C. | $\frac{1}{20}$ | D. | -$\frac{1}{20}$ |
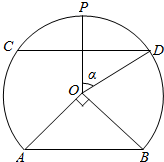 如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.
如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.